Part XI

Nov. 2020

The “Dark” Matter: Its Rarefaction Origin and Nature; Visible to Dark Matter Interactions and Transformations

Three Cosmic Equations of State: Visible Matter, Dark Matter and E/M Radiation

“Dark” E/M Radiation

The Possibility of Detecting

‘Visible to Dark’ Matter Transformations

Some Cosmological Adjustments

Contents

1. Introduction

2. Properties of Three Main Equations of State

General

Equations of State

The Curvature Criterion

3. The Elliptical Dark Matter State ( p² /b² + v² / a² = a²b²): The Dark Matter as a Rarefaction ‘Form’

General

Proposed Elliptical Equation of State for Dark Matter

Properties of the Proposed Elliptical Dark Matter

4. The Linear State: ‘Dark ‘ E/M Rarefied Radiation, Does It Exist?.

5. The Possibility of Visible-to-Dark Matter Transformations

6. Some Cosmological Consequences

7. Summary

Appendix A: Formation of Visible Hadronic and Leptonic Matter in a Hyperbolic Compressible Shockwave Appendix B: Outline of Compressible Flow and Shockwaves Appendix C: Transverse Waves in a Tenuous Fluid

1. Introduction

In Part X: The Big Bang: Visible Matter and Dark Matter Origins] [ Feb. 2020] [1] ,we re-examined our earlier proposal that visible cosmic matter (hadrons and leptons) are compression, dynamic forms which originated at the Big Bang in a hyperbolic compression shockwave, and are also routinely formed by the same compression shock process in linear accelerators [2,3,4],

We then proposed in the same document that the dark matter of the cosmos consists of rarefaction, dynamic ‘forms’ which also originated in an elliptical rarefaction shockwave associated with the sudden inflationary expansion event which occurred immediately after the Big Bang. This would finally provide a reasonable explanation for the dark matter’s origin, general nature, and provide a physical reason for its apparent non-interaction with our visible matter world, ours being compressive and the dark world being rarefied.

We now continue our examination of rarefaction compressibility to yield more detail on the nature of the Dark Matter World including the possibility that a form of ‘dark radiation” exists and is its ‘illumination’, as well as a proposal for a visible to dark matter transformations.

First, we put this in context with a look at three cosmic Equations of State.

2.0 Properties of Three Main Equations of State

2.1 General

Equations of State are equations which link the thermodynamic ‘state’ variables of pressure, p, specific volume (v = 1/ρ) and temperature T. [www.enegycompressibility.info : Part VIII : Equations of State for Cosmic Fields: [Ref 13].

These “states” are the dynamic, compressible entities in which waves travel and in which shock waves of either compression or of rarefaction form and produce elementary forms or particles of matter, visible or ‘dark as the case may be, but which so far have appeared to be almost completely separate and noninteracting .

For example, we have (a) the Ideal Gas Law as the hyperbolic equation of state describing the production of visible matter [ pv = const. = RT] : (b) the elliptical equation of state [p²/b² + v²/a² = a²b² = const] which we propose to describe the dark matter of the cosmos., and (c) the linear equation [p = ±Av] which will be seen to describe both Maxwell’s Electromagnetic waves, as well as newly proposed ‘dark’ electromagnetic waves to irradiate the dark matter world.

These three equations of state are depicted on pressure p, versus –specific volume ( v = 1/ϼ) diagrams, as in Fig. 1, Quadrant 1.

I

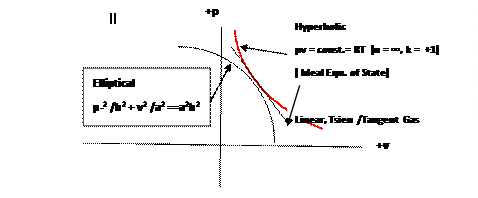
Figure 1: Equations of State for Visible Matter, Dark Matter and Linear Waves

2.2 Equations of State and Wave Types Supported by Each State:

(1) The hyperbolic state supports compression waves only; rarefaction waves die out but compression waves of finite amplitude grow to compression shocks. This state describes our visible or Hubble world in which the elementary particles of matter form in compression shocks.

The properties of our ordinary visible matter are, of course, well known and in voluminous detail. The state is one of condensed energy forms, i.e: elementary mass-particles, atoms, molecules.

For visible matter, the equation of state is hyperbolic: [ pv = RT = constant].

The visible matter interacts intimately with a linear wave state via the electro- magnetic force and via absorption and emission of condensed electromagnetic radiation ( i. e of photons).

(2) The linear state supports stable waves of both compression and rarefaction. Shocks cannot occur. The compression linear waves correspond to the stable E/M waves of our visible cosmos.

The linear equation of state [p = ±Av ±B] supports the condensed photons of electromagnetic radiation and its interaction with visible matter. Theoretically this equation also supports rarefaction waves and so the possibility of rarefied E/M radiation arises.

(3) The elliptical state, we now propose, pertains to the dark matter. This state supports rarefaction waves only. Waves of finite amplitude grow to form rarefaction shocks in which we propose dark matter ‘forms’ emerge to produce a rarefied kind of matter.

(Since the assigned elliptical equation of state for the dark matter supports only rarefaction waves and rarefaction shocks, any ‘forms’ would then necessarily be of ‘rarefied matter’, whatever this may mean. One might suspect that, because in our scheme the dark matter's rarefied state is opposite to the compressive state of our visible matter, that this might now explain the lack of any observed interaction of dark matter with condensed visible matter, as is currently the case.

Note: We should point out here that the three curves in Fig. 1 are for illustration of equation type only. That is to say, the relative sizes of the areas ( pv) under each curve ( pv represents an energy amount) are not representative of actually existing relative total energies; this would require expert assessment.

2.3 The Curvature Criterion for the Three Equations of State [Ref. (5) Shapiro. Vol. 1]

Pulses or changes in flow rate in compressible fluids cause pressure fluctuations which result

in traveling disturbances called pressure waves. These waves can be of either compression or rarefaction depending on the physical nature of the compressible fluid as expressed in its equation of state. Waves in material gases of visible matter (hyperbolic equation of state) are always compression while rarefaction waves are damped and die out. For the elliptical state the reverse is the case and rarefaction waves prevail.

If the wave amplitude is ‘infinitely’ small, the waves are stable and are called ‘acoustic waves’. If the wave amplitude is finite to begin with then, in both the hyperbolic and elliptical states, the waves grow rapidly to form shocks or shock wave, respectively of compression and of rarefaction.

The criterion for wave behavior is the curvature of the equation of state [d²p/dv² ] on the pv diagram.

P

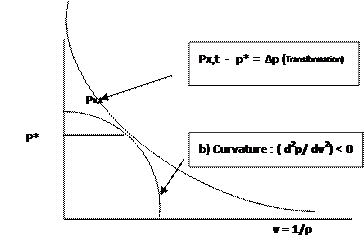
Fig. 2. Hyperbolic and Elliptical Equations of State with opposite curvature

1. If the curvature is positive [d²p/dv² > 0] as in the hyperbolic, visible matter case, then the compression waves are non-linear and steepen with time to form compression shocks; rarefaction waves die out.

2. If the curvature is negative [d²p/dv² ‹ 0], as in the elliptical dark matter, then their rarefaction waves are non-linear and steepen with time to form rarefaction shocks while compression waves die out.

[Note: In all states, if the pressure disturbances are of infinitesimally low amplitude then stable waves of either compression or rarefaction called acoustic waves can persist without growing to shocks].

3. In the case where the curvature is zero [d²p/dv² = 0], the pv curve is linear , i.e. it is a straight line, [p = ±Av ±B] and waves of both compression or rarefaction, and of any amplitude large or small, are all stable and can propagate unchanged. This linear case can also be visualized as the tangent case linking the hyperbolic and elliptical state equations.

To repeat, waves large or small, in this linear state, are all stable and all can propagate unchanged. Growth to shock waves is not possible in the linear case. [Ref. (5) Shapiro. Vol. 1]

3. The Elliptical Dark Matter State ( p² /b² + v² / a² = a²b²) : The Dark Matter Seen as Rarefaction 'Forms' or Rarefaction ‘Substances’

3.1 General

As we have shown in Part X, the formation of the elementary particles of our visible universe

can be described by compression shocks in the hyperbolic state [pv = constant] occurring in the Big Bang event.[1,4].

We now propose that the dark matter’s elliptical state should produce rarefaction shocks and rarefaction forms, and that this rarefaction property --as opposed to compression properties-- may then explain both the dark matter’s invisibility and its apparent non-interaction with visible forms of matter, except by way of gravity.

Our elliptical equation of state for the dark matter is :

P² /b² - v²/a² = a²b²⁼

/.

If the curvature is positive [ d²p/dv² › 0] as in material gases, then hyperbolic state compression waves steepen to form compression shocks and rarefaction waves die out.

If the curvature is negative [d²p/dv² ‹ 0], as in the proposed elliptical dark matter case, then rarefaction waves would steepen with time to form rarefaction shocks while compression waves would die out.

P

Fig. 3. Hyperbolic and Elliptical Equations of State with opposite curvature

We understand a great deal about ordinary hyperbolic matter ( 4.9% of the cosmos), but very little about the much more abundant dark matter (27%). The dark matter apparently occurs everywhere and has a strong influence on the structure, dynamics and the physical evolution of the cosmos. It does not appear to interact with ordinary matter, nor with electromagnetic radiation. Its interaction with our ordinary matter is apparently only by gravitation, although there is some thought that the dark matter may interact very weakly with matter by some application of the weak nuclear force.

Some other explanatory candidates have been that the dark matter is some new kind of unknown baryonic elementary particle, or involves weakly interacting WIMPS. Currently theories also distinguish between Cold, Warm or Hot Dark Matter.

However, ln this Report we have assigned to the dark matter a rarefaction nature, with its cosmic origin being at a strong rarefaction shock wave occurring in the sudden and massive inflationary expansion that occurred right after the Big Bang’s enormous compression state.

As a background to this new rarefaction shockwave proposition, we mention that we have earlier proposed that the ordinary matter’s elementary particles are routinely formed in compression shockwaves in linear accelerators, and that this is verified in the predicted mass ratios which are in good agreement with the experimentally measured mass ratios. [Appendix A: Formation of Visible Baryonic Matter in a Hyperbolic Compressible Shockwave]

I

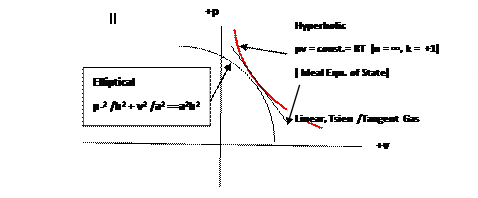
Figure 1: Equations of State for Visible Matter, Dark Matter and Linear Waves

4.0 The Linear State: Dark E/M Rarefied Radiation, Does It Exist?

The linear state equation [ p = ± Av ±B] is pre-eminently a stable wave equation. These linear waves can be of either compression or of rarefaction, but all are stable, propagating without change in amplitude, so that shocks are impossible. The linear compression waves interact with our compression visible matter as observable E/M photonic radiation.[17].

It seems reasonable therefore to propose then that there may also exist linear ‘dark’ rarefaction wave forms i.e. ‘rarefied photons’ which parallel the linear E/M compression photons which interact with our compression visible matter as E/M radiation.

A further question which arises is whether rarefied dark matter can interact with rarefied linear radiation? This would parallel the interaction of visible compression matter with the Maxwell’s compressed photonic electromagnetic linear radiation [ 17]. If so, the resulting ‘dark matter’ and its associated ‘dark’ radiation’ World would lie all about us. It is known through its gravitation to be five times as abundant as our own visible world, but it is as yet undetectable by any known means apart from its mentioned gravitational attraction. [

This then raises the possibility that a ‘dark linear E/M to dark matter interaction’ may be detectible by some means yet to be discovered.

To summarize: The linear equation of state [p = ±AV] is here taken as describing sets of linear waves, not only of photonic compression but of ‘photonic’ rarefaction as well. And so, we may now explore the possibility that “dark” leptons expressing ‘dark’ electromagnetism may also exist.

The proposal is a valid scientific proposition. It does however as yet lack some testable effects. We suggest that such effects may lie in some small numerical discrepancies in the experimental data of existing cosmological and quantum experimental testing.

5.0 The Possibility of Visible to Dark Matter Transformations: Is the Concept of Dark Energy Necessary?

Astronomical observations, of a large increase in the Cosmic Microwave Background Radiation ( CMB) discovered \around 1998. was interpreted as showing the universe to be undergoing an accelerated expansion. In explanation, the concept of an all pervasive “dark energy” exerting an expansion pressure was introduced. The amount of this new hypothetical energy needed to explain the CMB increase was enormous, constituting some 69% of the known universe compared with only 4.9% for the visible universe.

Towards a simplification, we now propose a transformation from World A matter to World B matter.

A Possible Transformation from Visible Matter to the “ Dark Matter”

. This transformation of World A visible matter to World B dark matter A would logically take place at a common tangential point having a common critical pressure p* ( Fig. 3.).

Fig. 3. Hyperbolic and Elliptical Equations of State with opposite curvature

Right after the Big Bang ,when the overall pressures in World A were very much higher than p* , the proposed transformation could only take place locally, as in astronomical vortices where the local vortex central pressure might drop low enough to reach the critical pressure p*. Such transformation vortices, if they exist, would probably be found in the center of quasars and in ‘Black Holes”.

To repeat, with an overall pressure lowering due to cosmic expansion, at some time in cosmic history the pressure in the core of a celestial vortex could conceivably drop locally to reach the cosmic pressure p* and then a local transformation from our World A (visible) matter to World B (dark) matter could take place. In other words, the vortex central core would become a local transformation sink in which the proposed transformation of visible matter to dark matter could occur locally. [Fig 2]. This transformation would be accompanied by an energy change. Such a Visible -to- Dark Matter Transformation Would Eiiminate the Need to Postulate A “Dark Energy” Solution

The energy change ∆ E in the A to B transformation is given by subtracting the two compressible energy equations∆E = c_B² – c_A² = V² [ 1/n_A - 1\n_B ]. And since n_A in our visible World is positive and n_B in the Dark Matter World would be negative, energy must be evolved in the transformation.

Now it would seems reasonable that this evolved energy ∆E would lie in the microwave range . This is because a rarefaction change in structure in the transformation would involve a molecular bond rearrangement and bond rotations have energies in the microwave range. Such a local rarefaction transformation and microwave energy release would then be detectable astronomically as a local increase in the Cosmic Microwave Background. (CMB)

The physics and astrophysics of quasars is complex and specialised. However, the presence of microwave radiation emissions in quasar cores is suggestive of molecular bond rotations such as would be expected or even essential in a (compressed) matter to “dark” (rarefied) matter transformation. It would thus appear that the available astronomical spectrographic observations on quasars may already constitute an experimental verification of the proposed transformation, but this is a matter for specialists.

At some era, with the progress of expansion to lower and lower cosmic pressures, the local transformation and local CMB shift in vortices could become more and more widespread, giving give the false impression that an overall acceleration in cosmic expansion rate was under way instead.

With the observed cosmic acceleration in expansion rate explained in this way as a consequence of visible to dark matter transformations and release of bond rotation microwave radiation, there would be no need to invoke “dark energy “. This proposal,‘ of course, needs quantitative study by cosmic radiation experts.

[Notes:

1. If the pressure in a laboratory vortex could be lowered to the cosmic critical pressure p* , it might be possible to bring about laboratory -scale transformation for a direct experimental verification of the transformation proposal.

2. At some future distant time, with continued hyperbolic state cosmic expansion, the overall cosmic hyperbolic pressure might reach p*, and then a general transformation of World A into World B matter might conceivably take place.]

6.0 Some Cosmological Adjustments

The Principle of Compressibility in Physics

The physical principle of compressibility runs through much of physics as a unifying concept and as a source of many unique explanatory instances. It may be well to list some of these qualities since they form the basis for an adjustment to physical cosmology:

In quantum physics, compressibility derives: The Lorentz Contraction Factor, Lorentz Invariance, wave/particle duality etc.[1]

In Electromagnetism, it fits Maxwell equations. the radiation wave speed wave speed, etc.[1] In particle physics it predicts the formation of visible elementary particles at a compression shockwave and the predicted particle mass-ratios match the measured ones.[2]

In current Cosmology it describes:

A physical mechanism for the Big Bang ,

A new explanation for the observed increased acceleration of the cosmic expansion as revealed by the CMB, and an elimination of the need for dark energy postulate

A Dark Matter interaction with the visible Hubble world at a critical cosmic pressure p*, and the possibility of its detection

Local transformations of visible matter into dark matter in the vortex core of quasars ,galaxies, etc.

Possibility of direct verifications of the transformation proposal in very low pressure vortices in the labo4ratory.

.

A physical basis for General Relativity and for Lorentz correction factors [1].

The problem of the discrepancy in vacuum energy density between physical cosmology on the one hand, where it is so low, and the quantum vacuum on the other where it is calculated to be enormously greater, now vanishes in compressibility cosmology because the two states are now physically separate and simply not comparable. Separateness as a solution for the problem has been suggested before; here we base it in the ‘separateness’ of the two physical states, respectively of hyperbolic flow and of linear flow.

The compressibility principle applied to cosmology provides not only a new unity, new explanations for current problems, but also new predictions for experimental validation tests.

The possibilities discussed, if eventually validated, will result in a simplification of physical cosmology on one hand, and an elaboration of details on the other.

7.0 Summary:

First, our new model would apply compressibility theory so that the Big Bang Initial Event becomes a physical compressive strong Shock Event, immediately followed by an inflationary rarefaction /expansion strong shock. The compression is governed by a hyperbolic equation of state, while the inflationary expansion is described by an elliptical equation of state. The compression shock produces elementary particles of visible matter; the inflationary/rarefaction shock, we theorize produces ‘dark matter’ particles.

Second, quantum effects, electromagnetism and radiation, both visible and dark, are described by a linear cosmic equation of state.

Third, universal gravitation as described by General Relativity is derivable from compressibility, which governs all three equations of state, hyperbolic, elliptical and linear. Its force can be expressed in compressibility terms as a pressure gradient force, but this remains to be developed.

Fourth, what has been prominently missing in current cosmology is any interaction of visible matter with the much more abundant cosmic dark matter. Now however, in the proposed model, interactions between quantum waves/particles and electromagnetism do continually take place between the hyperbolic and the linear state. In addition to what may have taken place universally in the Big Bang, ‘visible matter to dark’ matter transformations may also take place locally in regions of sufficiently low vacuum pressure (p = p*); such low-pressure sites would be in the cores of cosmic vortices such as in quasars, galaxies, and in Black Holes and the like. Energy would be released to the vacuum in such transformations, which released energy may be detectible as fluctuations in the Cosmic Microwave Background CMB, which could account for the observed acceleration in the expansion of the cosmos. If this mechanism is verified, it would eliminate the necessity for introduction of the controversial “dark energy’ to explain an inferred acceleration in the cosmic expansion rate.

Fifth, other currently unsolved problems such as Ultra Luminous X-ray sources (ULX’s) and Fast Radio Bursts (FRB’s) may also yield to an application of the new compressibility model.

Sixth, in addition to such astronomical confirmatory observations, there is also the intriguing possibility of direct experimental confirmation of the proposed visible to dark matter transformation by sufficient experimental pressure lowering, as for example in high speed vortices in laboratory accelerators.

Seventh, in the new cosmological model there is a wave speed limit. (i.e. speed of light limit). In addition, there is a limiting particle velocity at an “escape speed to a vacuum. ‘This particular compressible flow concept may be relevant to various current problems with Event Horizons.

References.

1. www.energycompressibility.info, Part X: The Big Bang: Visible Matter and Dark Matter Origins, Posted Feb. 2020

2. Power, Bernard A., Unification of Forces and Particle Production at an Oblique Radiation Shock Front. Contr. Paper No. 462. American Association for the Advancement of Science, Annual Meeting,+ Washington, D.C., Jan. 1982.

3.---------------, Baryon Mass-ratios and Degrees of Freedom in a Compressible Radiation Flow. Contr. Paper No. 505. American Association for the Advancement of Science, Annual Meeting, Detroit, May 1983.

4.. .---------------, Summary of a Universal Physics. Monograph (Private distribution) pp 92. Tempress, Dorval, Quebec,1992

5. . Shapiro, A. H. The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 vols. John Wiley and Sons, New York, 1951

6. Courant, R. and Friedrichs, K. O. (1948). Supersonic Flow and Shock Waves. Interscience, New York.

7. Lamb, Horace., Hydrodynamics 6^th ed. Dover, New York, 1932.

8. Chaplygin, S., Sci. Mem. Moscow Univ. Math. Phys. 21 (1904).

9. Tsien, H. S. Two-Dimensional Subsonic Flow of Compressible Fluids, J. Aero. Sci. Vol. 6, No.10 (Aug., 1939), p.399.

10.Bachall, N.A., Ostriker, J.P., Perlmutter, S., and P.J. Steinhardt. The Cosmic Triangle: Revealing the State of the Universe. Science, 284, 1481 1999.

11.Kamenshchick, A, Moschella, U., and V. Pasquier. An alternative to quintessence. Phys. Lett. B 511, 265,

12.Bilic, N., Tupper, G.B., and R.D. Violier. Unification of Dark Matter and Dark Energy: The Inhomogeneous Chaplygin Gas. Astrophysics , astro-ph/0111325. 2002.

13.www.enegycompressiility.info : Part VIII Equations of State for Cosmic Fields: Appendix C. Maxwell/s Electromagnetic Waves and Compressible Flow. Posted 2017.

APPENDIX A

Formation of Visible, Hadronic and Leptonic Matter in a Hyperbolic Compressible Shockwave

Evidence for the Origin of Baryonic Matter by Energy Compressibility in Shock Wave Condensations, as occurs in Linear Acelerators

We have earlier proposed .[1,2,3]. that : All elementary particles of matter (with the possible exception of the neutrino) are condensed energy forms produced under hyperbolic equations of state by compression shocks

The forms are given in terms of a simple, integral number n ( n = degrees of freedom of the compressible energy flow, which is roughly the number of ways the energy of the system is divided).. The experimental values of the ratio of the masses to one another are then related to the maximum theoretical compression ratio for each compression shock. ( Eq. 16 below). The observed fit is to within 1%.

A. Formation of Baryons and Heavy Mesons) in a Linear Accelerator Flow

Maximum Compression Ratio

m_b/m_q = V_max/c* = [n+1]1/2 (16)

m_b is the mass of any hadron particle, m_q is a quark mass, V_max = c_o n^1/2 is the escape speed to a vacuum; that is, it is the maximum possible relative flow velocity in an energy flow for a given value of n, the number of degrees of freedom of the energy form, This is a non-isentropic relationship which corresponds physically to the maximum possible strong shock.

Experimental verification values for this hadron mass- ratio formula is given in Table A below. (See

Appendix B: The Production of Visible Matter at a Strong Condensation Shock in a Linear Accelerator )

Table A) Hadrons (Baryons and Heavy Mesons)

-------------------------------------------------------------------------------------------- n n +1 [n+1]^1/2 Particle Mass (m_b) Ratio to

( MeV) quark mass

_____________________________________________

0 1 1 quark (ud) 310 MeV 1 quark (s) 505

1

2 3 1.73 eta (η) 548.8 1.73

3

4

5 6 2.45 rho (ρ) 776 2.45

6

7

8 9 3 proton (p) 938.28 3.03 (1) neutron (n) 939.57 3.03

Λ (uds) 1115.6 2.97 (2)

Ξ^o (uss) 1314.19 2.99 (3)

9 10 3.16 Σ⁺ (uus) 1189.36 3.17 (2)

10 11 3.32 Ω^- (sss) 1672.2 3.31 (4)

Note: Average quark mass is 310 MeV; (2) Average quark mass is (u + d+ s)/3 = 375 MeV (3) Average quark mass is (u+s+s)/3 = 440 MeV; (4) Average quark mass is 505 Mev.

Comparing column three, the maximum shock compression [n+1]^1/2 ], to the final column “Ratio to quark mass” we see that they closely agree, so that the proposed origin of hadrons by strong shock compression theory expressed in Equation 16 is verified.

B. Origin of Leptons, Pion and Kaon

m_L/m_e^- = k/α² = [(n+2)/n]/α² = {(n+2)/n] x 137 (17)

where α = 1/11.703 = [1/137]^1/2 is the fine structure constant of the atom , and k is the adiabatic exponent or ratio of specific heats, k = c_p/c_v = [(n+2)/n].

Because of the presence of k, this equation for the mass of the leptons is thermodynamic and quasiisentropic.

We propose that the leptons are formed via the weak shock option( i.e. they involve the reduction in strength of the fine structure constant [1/137]^1/2

The experimental verification for the lepton mass ratio formula of Eqn. 17 is given in Table B below.

Table B) Leptons, Pion and Kaon a

N k = (n+2)/n Particle Mass Ratio Ratio

(MeV) to x 1/137

Electron

__________________________________________________________

1/3 7 Kaon K^± 493.67 966.32 7.05

2 2 Pion π^± 139.57 273.15 1.99

4 1.5 Muon μ 105.66 206.77 1.51

- - Electron 0.511 1

Clearly, column 2 values for k ≈ m_l/m_e (1/137) closely match column 6 for the mass ratio reduced by 1/137, thus verifying Equation 17 and the theory that the leptons are formed by weak shock condensation. .

Summary

The problem of the origin of the observed mass-ratios of the elementary particles of matter to one another has here been explained by the compressible flow expressions to within about 1% of the experimentally observed values. This grounds the creation of matter in the strong compressible shock for the baryons, and in the weak shock option for the electron and leptons.

The principle of the compressibility of energy flow, therefore, would seem to underlie the emergence of material particles in the visible universe from some underlying energy field or continuum such as a modified general relativity field.

The above data are those of the standard model of elementary particle formation as verified in high energy accelerators. We now propose that this shock compression process for particle formation in accelerators may fit into the existing Big Bang model as well.

.References

1. Power, Bernard A., Unification of Forces and Particle Production at an Oblique Radiation Shock Front. Contr. Paper N0. 462. American Association for the Advancement of Science, Annual Meeting, Washington, D.C., Jan. 1982.

2.--------------, Baryon Mass-ratios and Degrees of Freedom in a Compressible Radiation Flow. Contr. Paper No. 505. American Association for the Advancement of Science, Annual Meeting, Detroit, May 1983.

3.---------------, Summary of a Universal Physics. Monograph (Private distribution) pp 92. Tempress, Dorval, Quebec,1992.

Copyright, Bernard A. Power, March 2020

Back to Top

Appendix B

( Excerpts from : Summary of a Universal Physics. Monograph (Private distribution) pp 92. Tempress, Dorval, Quebec,1992.]

2.0 Outline of Compressible Fluid Flow

The following is a listing of some relevant basic compressible flow principles. For more complete treatment see texts on compressible fluid flow or gas dynamics.[3, 4,5,6.7.8].

2.1 Steady State Energy Equation

c² = c_o² − V²/n (1)

where c is the local wave speed, c_o is the static [i.e at V = 0] or maximum wave speed, V is the relative flow speed, n is the number of ways the energy of the flow system is divided (i. e. the number of degrees of freedom) of the system and [ n = 2/(k− 1), where k = c_p/c_v is the’ adiabatic constant’ or ratio of specific heats.]

Here, ‘relative’ means referred to any (arbitrarily) chosen physical flow boundary. The equation is for unit mass, that is, it pertains to ‘specific energy’ flow.

The case where V = c = c* is called the critical state. The ratio (V/c) is the Mach number M of the flow. The ratio (V/c_o) is also a quantum state variable. The maximum flow velocity V_max (when c = 0) is the escape speed to a vacuum:

Vmax = √ n co.

2.2 Unsteady State Energy Equation

c² = co² – V²/n – 2/n (dφ/dt) (2a)

where φ is a velocity potential, and dφ/dx = u is a perturbation of the relative velocity. Therefore, in three dimensions, substituting V for u, we have dφ/dt = V (dx/dt) = Vc, and

c² = co² – V² /n − 2 (cV)/n (2b)

(See also sect. 3.2 below for far-reaching implications of the 2cV interaction energy term in quantum state physics).

2.3 Lagrangian Energy Function L

L = (Kinetic energy) – (Potential energy) = ( c²+ V²/n) – c_o² , and so, from (2b)

L = − (2cV)/n (3)

2.4 Equation of State for Compressible, Ordinary Matter Systems

The equations of state link the thermodynamic quantities of pressure p, specific volume (

volume per unit mass v = 1/ρ] and temperature T. The basic equation of state for ordinary gases is the equilateral hyperbola of the Ideal Gas Law:

pv = RT ; p/ρ = RT = constant (4)

Equation 4 is seen to be isothermal (T= constant) . For adiabatic changes it becomes pv^k = constant, where the adiabatic constant k = c_p/c_v is the ratio of the specific heats at constant pressure and at constant volume, respectively.

Here, each point on the curve presents the values for a particular pressure and volume pair and shows how the two relate to each other when one or the other is changed. In this hyperbolic equation, the product of the two -- i.e. the pv- energy -- has a constant value as set out by the equation of state.

p

Hyperbolic Equation of State (Ideal Gas Law)

Equations of State can be formed for gases, liquids or solids. Here, we shall be concerned mainly with those for the highly compressible states i.e. for gases.

2.5 Waves and Flow

2.5.1 The Classical Wave Equation

∆2ψ = 1/c2 [∂2ψ/∂t2] (5)

where ∆² = ∂²../∂x² + ∂²..^./∂y² + ∂²../∂z²; ψ is the wave amplitude, that is, it is the amplitude of a thermodynamic state variable such as the pressure p or the density ρ. The local wave speed is c.

The general solution of (5) is

ψ = φ₁ (x – ct) + φ₂ ( x+ ct) (6)

Equation 6 is a linear, approximate equation for the case of low-amplitude waves in which all small terms (squares, products of differentials, etc.) have been dropped.

The natural graphical representation of steady state compressible flows and their waves is on the (x,t), or space-time diagram.

t
	φ-
			x

The classical wave equation corresponds to isentropic conditions. It represents a stable, low-amplitude wave disturbance, such as an acoustic–type wave.

Unsteady State ( Accelerating) Compressible Flow

In compressible flow theory, forces, when present, introduce a curvature of the characteristic

lines for velocity on the space-time or xt-diagram. Space- time curvature thus indicates velocity acceleration and the presence of force .

(a) Straight characteristics and path lines show steady flow and absence of force.

(b) Curved characteristics and path lines show acceleration and presence of force

In the case of compressible flow and 3-space (x,y,z) , a curved path line dx/dt = v (path) may be ‘transformed away’ to a straight line Lagrange representation [ dh/dt = 0].

[Note: In General Relativity the analogous distortion of its 4-space (x,y,z,t) to obtain a force- free representation is a tensor distortion.

However, it should be noted that general relativity is a continuous field theory, and, as such, excludes discontinuities or singularities such as shocks. Therefore, it appears to be fundamentally incompatible with quantum physics.

On the other hand, compressible flow as shown below in Section 3.1 on Visible Matter predicts shock discontinuities as the physical mechanism for the emergence of the elementary particles of matter by shock compression of an energy flow. Thus, compressible flow is compatible with quantum theory whereas general relativity is not.]

2.5.2 The Exact Wave Equation

2 ψ = 1/c2 ∂2ψ/∂t2 [ 1 + ψ ](k + 1) (7)

where k, the adiabatic exponent, is k = c_p/c_v = ( n + 2) /n; and ( k + 1 ) = 2( n + 1)/n = 2(c_o/c*)². Here, pressure is a function of density only. This wave is isentropic, non-linear, unstable, and grows to a nonisentropic discontinuity called a shock wave.

2.5.3 Shock Waves

All finite amplitude, compressive waves are non-linear and grow in amplitude with time to form shock waves. These shocks are discontinuities in flow, across which the flow variables p, ρ, V, T and c change abruptly. (Note p = pressure, ρ = momentum).

2.5.3.1 Normal Shocks

V₁ > V₂ (8)

p₁, ρ₁, T₁ < p₂, ρ_2, T₂ (9)

Entropy Change Across Shock:

∆S = S₁ – S₂ = − ln(ρ₀₂/ρ₀₁) (10)

Maximum Condensation Ratio:

ρ₁/ρ₂ = [n+1]^1/2 = V_max/c* (11)

2.5.3.2 Oblique Shocks

If the discontinuity is inclined at angle to the direction of the oncoming or upstream flow, the shock is called oblique.

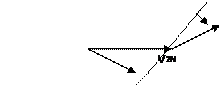
V1 V2

Oblique Shock V_1N > V_2N p₁ρ₁T₁ < p₂ρ₂

Since the flow V is purely relative to the oblique shock front, the shock may be transformed to a normal one by rotation of the coordinates, and the equations for the normal shock may then be used instead.

2.5.3.3 Strong and Weak Oblique Shock Options: The Shock Polar

For each inlet Mach number M₁ ( = V_N1/c), and turning angle of the flow θ, there are two physical options:

1) the strong shock ( intersection S) with strong compression ratio and large flow velocity reduction (p₂ >> p₁; V₂ << V₁, or

2) the weak shock (intersection W, with small pressure rise and small velocity reduction.

Which of the two options occurs depends on the boundary conditions: low back i.e. low downstream pressure favours the weak shock occurrence; high downstream pressure favours the strong shock.

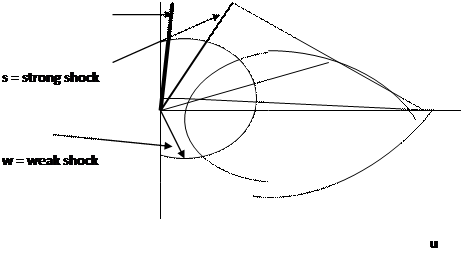
M* = v/c = 1 c*

When the turning angle θ of the oncoming flow is zero, the strong shock becomes the normal or maximum strong shock, and the weak shock becomes an infinitesimal, low-amplitude, acoustic wave.

2.6 Types of Compressible Flow:

a) Steady, subcritical flow ( e.g. subsonic, V< c), governed by elliptic, non-linear, partial

differential equations.

b) Steady, supercritical flow ( e.g. supersonic, V₁ > c) governed by hyperbolic, nonlinear, partial differential equations.

c) Unsteady flow (either subcritical or supercritical). These are wave equations governed by hyperbolic, non-linear, partial differential equations. They are often simplified to linear approximations, for example to the classical wave equation (5); if of finite amplitude they grow to shocks..

The solutions to the above hyperbolic equations are called characteristic solutions. If linear, they correspond to the eigenfunctions and eigenvalues of the linear solutions to the various wave equations of quantum mechanics ( Sect. 3.7), or, equally, to the diagonal solutions of the matrix equation of Heisenberg’s formulation of quantum mechanics.

2.7 Wave Speeds

c = [ c_o² – V²/n]^1/2 (steady flow) (12)

c = c_o² – V²/n – [(2/n)cV ]^1/2 (unsteady flow) (13)

c² = (dp/dρ)_s, where s is an isentropic state.

Since V is relative, it may be arbitrarily set to zero to give a stationary or “local” coordinate system moving with the flow; this automatically puts c = c_o and transforms the variable wave speed to any other relatively moving coordinate system.

The shock speed U is always supercritical (U > c) with respect to the upstream or oncoming flow V₁.

2.8 Wave Speed Ratio c/c_o and The Isentropic Thermodynamic Ratios

c/c_o = [1 -1/n(V/c_o)²]^1/2 = (p/p_o)^1/(n+2) = (ρ/ρ_o)^1/n = (T/T_o)^1/2 (14)

All the basic thermodynamic parameters of a compressible isentropic flow are therefore specified by the wave speed ratio c/c_o. .

2.9 Relativity Effects in Compressible Flow: In compressible flows all velocities [V or u] are relative only, and, moreover, the wave speed c is a variable which is dependent on V and n; it decreases for larger velocities V. and it reaches its maximum value c_o at the static state i.e. at zero flow (V =0).

Interestingly, Equation (14)

c/c_o = [1 -1/n(V/c_o)²]^1/2 = (p/p_o)^1/(n+2) = (ρ/ρ_o)^1/n = (T/T_o)^1/2 (15)

shows that the correction factor for the effect of flow speed on wave speed c on the right hand side of the equation has the same form as the Lorentz Transformation of special relativity. If n = 1 the two correction factors become formally identical.

The differences from special relativity are that the wave speed c is now a variable and a function of the flow velocity V, and that there is the energy partition constant n. Since the wave speeds are low ( c = 334 m/s for air at m.s.l.), the ‘Lorentz’ corrections for physical compressible systems such as gases are relatively large. Also, the flow speeds can exceed the wave speed ( supersonic flow), whereas in special relativity theory, the wave speed c is a constant ( 3 x 10⁸ m/s) which can never be exceeded.

Photon shocks are thus impossible in special relativity, whereas in compressible flow they furnish a quantum physical theory for the origins of matter itself via the formation of the elementary particles of matter at compression shock discontinuities.

2.10 Wave Stability

Compression waves are the rule in the baryonic physical world ( i..e. in Quadrant I on the pressure-volume diagram) where density waves are always compressive and all compression waves of finite amplitude grow towards shocks. Here, only acoustic compression waves ( i.e. infinitely low-amplitude compressions) are stable.

Finite rarefaction waves and rarefaction shocks are impossible in material gases; only infinitely lowamplitude rarefaction waves can persist.

We shall see below that, with elliptical equations of state ( dark matter) and linear equations of state ( quantum radiation), stable, finite rarefaction waves do become possible.

2.11 Elliptical Equations of State and Rarefaction Waves

Elliptical Equation of State favours Rarefaction Waves and Shocks

The criterion for wave behaviour [4] is the curvature ( dp/dv) of the isentropic equation of state:

1. If d²p/dv² is > 0 (i.e. the hyperbolic curve) compression waves form and steepen, while rarefaction waves flatten and die out. Only compression waves of infinitely small amplitude (“acoustic” or “sound” waves” ) are stable.

2. If d²p/dv² is < 0 , ( i.e. the elliptical curve) rarefaction waves form and steepen, while compression waves flatten and die out.

.

We therefore see that ordinary gases are hyperbolic and favors compression waves and compression shocks. No real gas is known whose equation of state is elliptical and favors’ rarefaction waves; but we are now proposing that itiis thus elliptical relationship which furnishes the hat it is this elliptical relationship which furnishes the Equation of State for the Dark Matter of the Cosmos. We are also

proposing that the third option, namely the linear state fits the quantum world aand the Electromagnetic state.

Back to Top

Appendix C

Transverse Waves in a Tenuous Field:

Maxwell’s Electromagnetic Waves and Compressible Flow

Compressibility and Electromagnetic Waves : Evidence for transverse waves in a tenuous fluid

Here we shall show that compressible flow theory and the two proposed orthogonal linear equations of state p = ± v can produce transverse waves in a shear free compressible fluid, so as to fit with the established transverse nature

of electromagnetic waves.

( The following insert is from UF pages) needs editing to fit in here,,

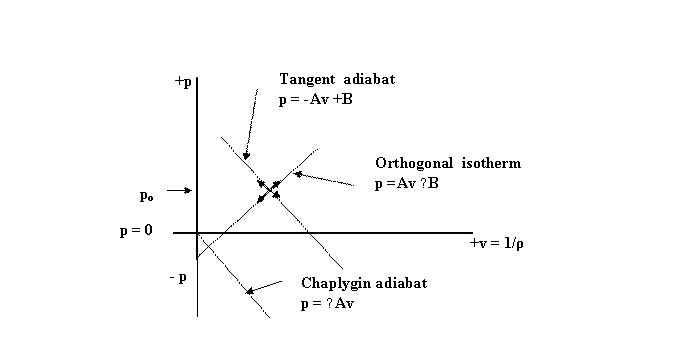
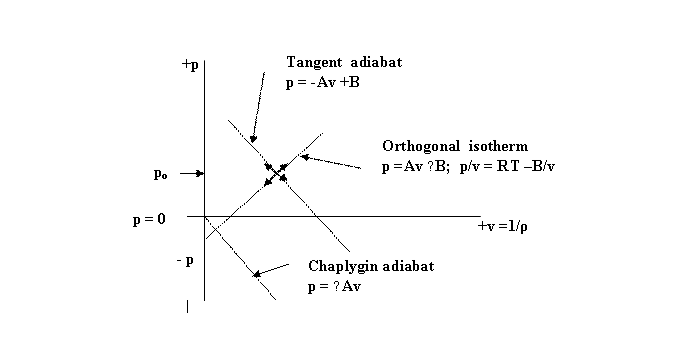
Material gases, being tenuous fluids, can only support longitudinal waves, that is to say, waves in which the density variations ±∆ρ are along the direction of wave propagation. They cannot support transverse waves in which the density variations would be transverse to the direction of wave propagation. Its was this inability of a tenuous medium to transmit the transverse waves of light which led to the demise of the old luminiferous ether concept. We now ask: What is the evidence for transverse fluid waves in the Linear Wave Field with its mutually orthogonal adiabatics and isotherms?

We consider a simple pressure pulse ( ±∆p) in the orthogonal wave field:

A pressure pulse ( ±∆p) in the Orthogonal Wave Field

The initial or static state is designated as p_o. When the pressure pulse ( +∆p) is imposed from outside in some way, the wave field must respond thermodynamically in two completely orthogonal and hence two completely isolated ways, namely, by (1) an adiabatic stable wave along the adiabatic( TG) and (2) by an isothermal stable pulse along the isotherm (OG).

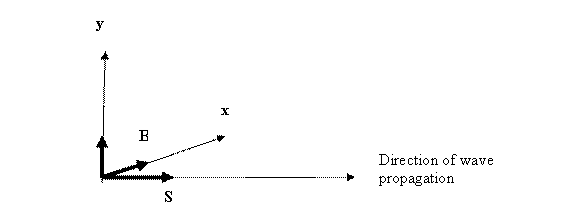
Spatially, the constant pressure disturbance ( +∆p) must propagate in the direction of the initial impulse ,but, since the there are two orthogonal components of the pulse are the only way for this to take place is for the two mutually orthogonal components to also be transverse to the direction of propagation of the two pressure pulses. Vectorially, this requires an axial wave vector V in the direction of propagation ( say z) with the two pulses orthogonally disposed in the x-y plane. i.e. TG x OG = V which is reminiscent of the Poynting energy vector S = E x B in an electromagnetic wave.

E

Electromagnetic Poynting energy /vector

A wave of amplitude ψ traveling in one direction (say along the axis x) is represented by the unidirectional wave equation

dψ/dx = 1/c dψ/dt

Maxwell’s electromagnetic waves

Here, however, in the case of our adiabatic and isothermal pressure pulses we have two coupled yet isolated unidirectional waves, and this reminds us of Maxwell’s coupled electromagnetic waves for E and B, as follows

dE_y/dx = (1/c) dB/dt and dB_y/dx = (1/c) dH/dt

where c is the speed of light, E is the electric intensity and B is the coupled magnetic intensity.

Maxwell’s E and B vectors are also orthogonal to each another and transverse to the direction of positive energy propagation.

Therefore, we have formally established in outline a two component wave system in theLinear Wave Field with (k = −1) which formally corresponds to the E and B two component orthogonal system of Maxwell for electromagnetic wave propagation through space in a continuous medium. His equations for E and B are

Curl E = ∂E_y/∂x = −(1/c) ∂B/∂t

Curl B = ∂B_y/∂x = − (1/c) ∂E/∂t

If we now designate our Tangent gas as A ( for Adiabatic) and our Orthogonal gas as I ( for

Isothermal) then our analogous wave equations would be

Curl A = ∂A_y/∂x = − (1/c) ∂I/∂t

Curl I = ∂I_y/∂x = − (1/c) ∂A/∂t

The two systems are formally identical. Therefore, we propose that the medium in which Maxwell’s transverse electromagnetic waves travel through space is to be physically identified as a Linear Wave Field, having the above described thermodynamic properties for adiabatic and isothermal motions initiated in the wave field and initiated by pressure pulses ( presumably by accelerated motions of electric charges.) The compressibility of the wave state now accounts on physical grounds for the finite wave speed ( speed of light), and in addition wave motions in this tenuous fluid medium are transverse, as required by the observations..

It is possible to reduce Maxwell’s two equations UF equations to a symmetrical single wave equation

∂²E/∂x² = (1/c²) ∂²E/∂t²

∂²B/∂x² = (1/c²) ∂²B/∂t²

and similarly with A and I for our Adiabatic/Isothermal coupled wave in the UF:

∂²A/∂x² = (1/c²) ∂²A/∂t²

∂²I/∂x² = (1/c²) ∂²I/∂t²

This is not surprising since the UF with its k = −1 thermodynamic property is the unique compressible fluid which automatically generates the classical wave equation with its stable, plane waves. The formal agreement of the UF theory with Maxwell is again striking.

Instead of taking our initial external perturbation as a pressure pulse ( +∆p) we should more realistically, from the physical standpoint, take it to be a density condensation (s = ( ρ – ρ_o ) / ρ_o = +∆ρ/ ρ_o). This will now result in a positive pressure pulse (+∆p) appearing in the adiabatic (TG) phase of the UF but a negative pressure pulse ( −∆p) in the isothermal or orthogonal perturbation component (OG) . This perturbation is represented by the two orthogonal sets of arrows on the pv diagram, one corresponding to +∆p and the other set corresponding to − ∆p. As the wave progresses the two orthogonal vectors also rotate.

S

The physical ambiguity which results from a pressure/density perturbation in the Orthogonal UF

An oscillating density perturbation ( ±∆ρ) then results in an axial wave vector having two mutually orthogonal components ( adiabatic and isothermal ) in a density perturbation wave. This appears to correspond formally to the Maxwell electromagnetic wave system with its two mutually orthogonal vectors for electric field intensity E and magnetic field intensity B.

We have thus established a case for the compressible linear wave field being a cosmic entity which transmits transverse electromagnetic waves through space. A necessary

next step will be to examine the field or state in relation to all the

multifarious established facts relating to electromagnetic radiation.. These must include the nature of electric charge, electrostatic fields, the compressed fields of moving charges and the resulting magnetic fields, etc. etc. Preliminary work has indicated that this additional reconciliation will be successful.

Nite: The appropriate wave equation for the compressible flow field, from which the quantum shock compressions that generate the elementary particles of matter are produced, would seem to be the exact Classical Wave Equation:

2 ψ = 1/c2 ∂2ψ/∂t2 [ 1 + ψ ](k + 1)

where k, the adiabatic exponent is c_p/c_v = ( n + 2) /n; and ( k + 1 ) = 2( n + 1)/n

= 2(c_o/c*)². Here, pressure is a function of density only. This wave is isentropic, non-linear, unstable, and grows to a non-isentropic discontinuity called a shock wave. It is at these shock discontinuities that the elementary particles can form – the hadrons at the strong shock and the leptons at the weak shock option.

In many quantum actions stable waves are involved, such as the electromagnetic waves. For these we propose the linearized classical wave equation, as follows

∆2ψ = 1/c2 ∂2ψ/∂t2

where ∆² = ∂../∂x² + ∂^2../∂y² + ∂²../∂z²; ψ is the wave amplitude, that is, it is the amplitude of a thermodynamic state variable such as the pressure p or the density ρ. The local wave speed is c.

The general solution is

ψ = φ₁x – ct) + φ₂( x = ct)

This equation is a linear, approximate equation for the case of low-amplitude waves in which all small terms (squares, products of differentials, etc. have been dropped.

Summary

We have presented examples of a close conection of compressible flow theory and quantum mechanics fundamental relationships. We have related the formation of the elementary particles of matter to energy condensation occurring in compression shocks in a compressible flow.

We have assigned a Linear Equation of State to the quantum fields of

electromagnetic radiation. This equation has two forms, one being adiabatic and the other being isothermal. In the case where these two equations are orthogonal. the resultant wave would appear to be transverse to the direction of motion.. Then, the transverse wave equations are shown to formally match Maxwell’s electromagnetic equations.

Copyright, Bernard A. Power, September 2017

Back to Top