Feb.2 /2019

Part IX

A Human Equation of State at a Thermodynamic Limit

A Scientific Requirement for Spirit?

Summary

A need in neuroscience, for a scientific theory to explain observations of brain temperature patterns and variations, points to a thermodynamic Equation of State. The classic one is the Ideal Gas Law [pv = constant]. This, however, has a requirement for an infinity for its variable n, the number of equal energy states, and so it is is always used in physics as a close approximation only.

However, if applied to humans under the classical philosophic ‘body and soul’ theory of human nature, then the equation could fit exactly, because spirit in rational philosophy is intrinsically unquantified and can assume any value required.

This is rather startling, as is the fact that the predictions of such a Human State Equation would be readily verified or falsified by observation. Thus, a canonical scientific theory, which is predicated on a spiritual essence for human nature, exists.

Experimental verification of the theory with human neurological and cognitive data is discussed.

Contents

•Introduction to a Thermodynamic Problem

•Thermodynamic Equations of State

•Proposed Unique Solution: An Ideal/ Isothermal Human Equation of State at a Thermodynamic Limit

• Properties of The Proposed Human Thermodynamic State

•Experimental Verification of the Proposal

• Relevant Further Questions

• Caveat

• Conclusions

• References

Appendix A: Outline of Compressible Fluid Flow

Introduction to a Thermodynamic Problem

In the course of a study of five cosmological fields, namely: ordinary compressed matter of the visible universe, the dark matter, dark energy, quantum and electromagnetic fields, and gravity [1, 2 3], a review was made of their respective thermodynamic equations of state. The simplest of these state equations is the hyperbolic equation pv = constant for the matter of the To repeatvisible cosmos. This equation is the familiar Ideal Gas Law which has such wide application in compressible fluid physics, gas dynamics and cosmology [4].

.

In a derivation, this same Ideal Gas Law, pv = const., emerges sequentially from the adiabatic gas equation series, pv^k = constant , at the theoretical limit where the adiabatic index k becomes equal to + 1 [ i.e. pv^k=1 = pv¹ = pv = const.] and the equation becomes simply pv =constant. However, since this also requires that n, the associated number of degrees of freedom, or number of ‘microstates’, must become an infinity [ n = 2/(k−1) = 2 / (+1 −1) = 2 / 0 = ∞], then the exact gas law is not physically possible; it evidently must exist only theoretically, or as a very useful approximation.

It seems, however, odd that such a fundamental scientific relationship as the ideal gas law must, strictly speaking, exist only theoretically, and so the matter was studied in some depth. To repeat, the derivation of the ideal law as the limit of the adiabatic series, where k, the adiabatic index, becomes unity, is ;

pv^k = pv^k=1 = pv¹ = pv = const.

But, at this limit, when k = +1, n becomes infinity, since n = 2/(k − 1) = 2/(1− 1) = 2/0 = ∞.

Since infinity is not possible in physical systems, it then seems clear that the exact ideal gas law can not actually exist in the physical cosmos.

Toward a possible solution, we first look at compressible flow and thermodynamic equations of state.

Thermodynamic Equations of State

Thermodynamic Variables

Compressible systems have the thermodynamic variables, specific density ρ, pressure p, specific volume v = 1/ ρ and temperature T (4).

The relationships among these thermodynamic state variables are given in an Equation of State.

The Ideal Gas Equation of State

Principal among the equations of state is the Ideal Gas Law, pv = constant. This state requires n = ∞, k = +1,

where k is the ratio of the two specific heats , k = c_p/c_v and is called the ‘adiabatic index,’ and n is the number of ‘microstates’ and is related to k as n = 2/[k − 1].

The Isothermal Equation

When the constant in the gas law, pv = const, is set to equal RT, with T as the temperature and R as the universal gas constant, then we get the isothermal equation of state:

pv = RT= const.

This equation also requires that n must equal infinity.

In physic,s this isothermal equation is applied to expansion or compression of gases which are immersed in an environmental heat bath to maintain the required constant temperature. Moreover, these processes are required to take place slowly enough to maintain this temperature constancy by heat diffusion into or out of the working gas.

In the proposed classical human ‘body and soul’ case, the behavior of the temperature during some human activities is likely to be unusual. As with all warm-blooded animals the human general body temperature is quasi- constant and may supply the equivalent of a general constant temperature heat bath. However, the restriction to an extremely slow reaction process may not apply, and would be a matter for observation and analysis. The effects on the stability of wavc types and their amplitudes could also be unusual in humans.

In general in both the ideal state and the derived isothermal state the waves are stable only if they are low amplitude acoustic types; finite waves are compressive , unstable and grow to shocks.

The Linear Wave “Tangent” Equation of State

The Linear Wave Equation of State is: p = Av + B , where A is a negative constant. It graphs as a straight line with negative slope on the pv diagram. When it is set tangent to the hyperbolic ideal gas law, it is known as the Tsien/ Tangent Gas [4] or ‘The Tangent Gas’. In the non- tangent case, it is called the Chaplygin gas (4).

A principal feature of this state equation is that its waves can be either compression or rarefaction types and they are uniquely stable at all amplitudes, large or small. Shocks are not possible. Since rarefaction waves are producers of negative entropy, this state is of obvious special interest to human neurology and cognitive science for possible intellectual applications.

This state occurs with k = −1 ;and n = −1 . Again, as with the infinity requirement for the ideal gas state, we have physically exotic or unrealizable values.

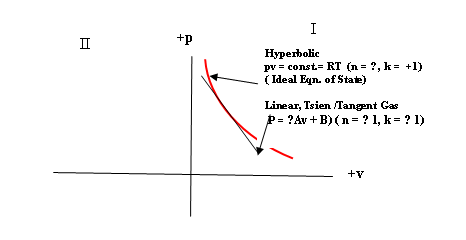
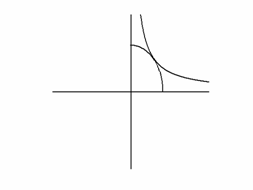
Fig. 1. Thermodynamic Equations of State: The Ideal Gas Law and the Linear, Tsien/ Tangent Equation

[Note: A more detailed outline of compressible flow matters is given in Appendix A: Outline of Compressible Fluid Flow]

Proposed Unique Solution:An Ideal Isothermal Human Equation of State at a Thermodynamic Limit

The Problem: This Proposed Ideal Human Equation of State, [ pv = const = RT] is only possible with n = infinity

To meet this requirement for an infinity, so that the ideal equation of state can actually exist, we note that philosophically, a spiritual dynamism has the property of being intrinsically unquantified. That is, spirit can accommodate any numerical value, including zero or infinity.

Now, over millennia, in classical and pre-modern times, we humans have been, on the rational evidence, considered to be ‘ body and spirit’ animals. Today, that logical rationality and its conclusion are still valid. [5, 5a]. Science, however, in addition to its rational theory, requires experimental verification as a prerequisite to acceptance of its proposals.

A Solution:

It is surely rational if we now propose, as a starter, that humans possess an ideal thermodynamic equation of state pv = const.

As we have seen, this equation requires an infinity for the state variable n, but if we further propose that humans are ‘body and soul animals’, then, since the proposed human spirit would be intrinsically non-quantified, it would be able to meet the infinity requirement for n, and so would qualify humans as unique embodiments of this thermodynamic equation of state.

This simple but demanding equation of state would then describe aspects of an inner state or inner core to our human activities, physical and intellectual. Remarkably, it also appears to be a true scientific proposal by being open to experimental testing for its acceptance or rejection. It may or may not be real, depending on the results of experiment data of human neurology and physiology.

In summary, a valid thermodynamic human equation of state of format, pv = constant = RT can now emerge, with n equal to infinity, if we adopt the rationally postulated spiritual dynamism or soul essence for human nature which can support this infinity requirement.

The logic and rational evidence of the classical and pre-modern philosophical position on the nature of man as a spiritual/rational animal has always been overwhelming. The rise of our scientific and technological way of life, however, has routinely excluded spirit from discussion because of its requirement for scientific proof, which requires experimental proof as well as logical, physical theory.

The proposed human equation of state pv = RT predicts thermodynamic and dynamical effects which, if real, will be observable experimentally. This particular, human ‘body and soul’ hypothesis is thus a scientific one.

[ Note: The Tangent, Linear Wave State [p = Av + B ] also requires physically unrealizable values of k = −1 ; n =−1 . This problem also vanishes, however, with the ‘body and spirit’ human nature case, since spirit can accommodate any physical value. Therefore. the Tangent State Equation is also available to serve as a Human Equation of State, and can be tested experimentally. We shall confine our attention here to the Ideal State Equation].

Properties of The Proposed Human Thermodynamic State

The Proposal: Neurology observes animal brain temperatures, variations and patterns, and a need has been expressed for a comprehensive explanatory theory. But, since temperature is a thermodynamic variable, then one appropriate comprehensive descriptor would be a thermodynamic Equation of State. [ Other theoretical approaches, such as heat and mass transfer theory, might also apply, but the ideal state equation with its direct links to oscillations, waves and entropy changes seems a better starting point] .

The most widely used Equation of State is probably the Ideal Gas Law: pv = const. = RT.

This equation is always used as a close approximation only, since the exact conformity would require an infinite numerical value for one state variable, namely for n the number of equal energy states or ‘microstates’.

Our proposal is that the Ideal Law would apply exactly to humans if their nature is taken as ‘body and soul’, that is to say , as in the classical definition. This proposal is also a scientific one, since it is open to experimental testing.

A Human Inner State: The next relevant question is :What is this “State” to which the Ideal Equation pv = c would apply? Is it, for example, a compressible medium of some special sort? A medium of what? A compressible energy field? A wave field ? An interaction field? A body and soul interaction energy field or state?

Let us look at the ‘body and soul interaction field or state’ choice . We have mentioned above that the interaction of a wave having velocity c with a flow having an impulse velocity u, produces a specific energy ( i.e. an energy per unit mass) E_sp expressible as:

E_sp= (c + u)² = c² + 2cu + u²

where the term 2cu representts an energy of interaction between wave speed c and the pulse velocity u

If now we postulate that the human soul, or spiritual human , induces the wave motion c and the body supplies the pulse action u, then the 2cu interaction energies summed over the entire body would form a new energy field or state, one that is a true human unity of spirit and matter, free of any Cartesian Dualism . The energy of the interaction field, E_{Ψ, might} then be expressed symbolically as:

E_{Ψ =} ∑ (2cu)

This energy field would form an inner statc, central to our human activities, physical, intellectual and spiritual.

If this 2cu energy is conceived of as a 2cu human field, analogous to an atom field , a molecular field, a quantum field, and etc. then we could conceive of it as an “interaction energy field’ or human compressible state to which the Ideal Law, pv = constsnt = RT, applies. This law would then describes the thermodynamic observables, i.e. temperature, entropy, pressure, specific volume and density, and would support the dynamic observables of wave action, oscillations, resonances and the like.

We emphasize that this inner field is neither a physical field nor a ‘soul field.’. Instead, it is a new interaction entity and field with its own observable thermodynamic and dynamic variables.

We might further envisage the living state as involving a constant generation of interaction energy, 2cu, as each atom, molecule, tissue or fluid pulsates, vibrates or flows. In non-human living things, these interactions would be purely physical waves and pulses interacting to produce a physical living being. With humans, the 2cV field relates to a new and distinct ‘soul and body’entity [5].

The Human Ideal thermodynamic Equation of State, pv = c, which requires an infinity for its ‘number of microstates’ or equipartition parameter n, could therefore describe exactly , i.e. without approximation , the thermodynamic and dynamic neurological and cognitive properties of a ‘body and soul’ human inner energy state or inner field.

Experimental Verification of the Proposal

A proposition is only scientific if, in addition to its rational, scientific logic or theory, there is also at least one experimental test open for validity or falsification.

Generally: Human neurological and cognitive observations [6,7] have established that humans possess thermodynamic elements e.g. (1) a quasi- isothermal body temperature, (2) brain temperature and fluctuations in its value, (3) brain or neural oscillations or wave motions

Furthermore, it has been reported [ 6,7] that some general theoretical scientific theory seems required to properly account for the neurological temperature field observed in the brain and for the observed temperature correlations with other brain properties.

Therefore, our present proposal that there is a human thermodynamic equation of state which embodies such thermodynamic properties, is a valid candidate to meet the expressed needs of the science for a suitable formal theory.

Principal Quantitative Observables: Brain temperatures and neural waves and oscillations would appear to be among the main observables.

Since the proposed equation of state has the isothermal form pv = RT = constant, then the stability of brain tempersture and the magnitude of thermal fluctuations in the human brain could quantitatively test the predicted isothermal behaviour under different physical and mental activitie. The correlations established would sharpen comparative data.

Neural waves and oscillations could now be studied for patterns of wave types and quantitative properties permitted by the proposed exact equation of state, such as frequency, amplitude, wave speed, etc.

Specifically; Some specific areas suitable for quantitative testing might include the following:

(a): A requirement to explain the existence and qualities of states of inner calm or serenity (8), which would appear to mesh with isentropic states of the state equation, pv = const. = RT.

(b): Orderly states for logical and intellectual activities. These might be accompanied by a stable rarefaction wave state which would mean an emergence of the decreased entropy or increased order, which is required.

(e): Wave types which would match various observed neural waves or oscillations. The isothermal state’s waves[ pv = RT = constant] should be stable for low amplitude acoustic type waves, but gives unstable compressions for large amplitude waves; the linear wave state [ p = Av +B] could match any desired stable wave type, compression or rarefaction.[See Appendix A: Outline of Compressible Fluid Flow Section 2.10 Wave Types and Stability].

[ We suggest that comparisons of humans with non-human primates will not provide a sustainable objection, since, for the other primates, a purely physical adiabatic equation of state [ e.g. pv^k>¹ = const.) with k greater then 1 and n less than infinity, may well exist to match their neurological and cognitive manifestations. The proposed differences for humans ought to be readily observable and verifiable].

[Note, that the inescapable inexactitude in observational data is not an obstacle to determining whether of not the proposed human equation of sate is intrinsically ‘exact’. All that is required is a unique degree of exactitude in the human case].

Relevant Further Questions

In General, further relevant matters which arise, are: :

(a): “The hard problem of human consciousness” in cognitive science.

,

(b ): The origin and nature of the universally experienced intellectual appetite or innate drive towards understanding in Science and Technology research (9).

(c): The nature and source of the “Eureka” Moments of “Joyous” Insight and Discovery which occur sporadically during intellectual and scientific investigations (9).

(d): Human Contemplative and Meditative States (6).

(e) The human sense of “self”, individuality, unity. and identity.

Thermodynamic Tests:

The observables here would seem to be principally body temperature and, especially, brain temperature.

Entropy change values would be readily available via temperature changes since the two are proportionally related.

This ideal, human equation of state should variously be thermodynamically entropic, isentropic or negentropic according to the particular human activity involved.

Thermodynamically, entropy/temperature signals should be related to neural signals and to harmonic neural oscillations.

Distinctive entropy changes, in particular any presence of a negentropy being associated with intellectual activities, would be of central importance.

Any temperature (entropy) effects accompanying the “Eureka Moments” of Insight that occur during research. .

Do the data fit so as to verify or suggest an exact Hunan Equation of State? [Note, that the inescapable inexactness in observational data is not an obstacle to determining whether of not the proposed human equation of sate is intrinsically ‘exact’. All that is required is a unique degree of exactitude in the human case].

Dynamic Tests:

Here we have the state equations’ wave speed values, and especially their unique wave properties. Many varied wave tests are possible, including a wide range of oscillations, resonances and pulses.

In neurological and cognitive science a massive amount of observational data is already available, and there is an expressed need for theoretical thermodynamic and oscillatory insight.

Finite, stable Wave Amplitudes

Absence of Shock Waves

Wave types: In the pv = consant state, low amplitude acoustic compressions would be the rule. Rarefaction waves are not possible.

In the pv = RT or isothermal state, stable waves of both compression or rarefaction may be possible, depending on the precise temperature control. The wave action in the exact human case nay be different than that in a purely physical, approximate case.

Wave types: In the linear State, both stable compressions and stable rarefactions of finite amplitude are present. The latter could give rise to negentropy. Shocks are ruled out.

A Caveat

Because of the highly unusual nature of the subject matter of the present report, it seems prudent to offer some cautions.

First, the views presented above are preliminary, conditional on a particular logical path chosen, and therefore tentative. That said, it is felt that they solidly support further investigation by neurologists, thermodynamicists, and physiologists, among others.

In addition to the pursuit of the Relevant Further Questions put forward above, there will arise, if the experimental data are supportive of the thesis, the interesting matter of the details of the unity of soul and body. I have mentioned the flow/wave pulse energy example (c + u )² = c² + u² + 2cu where the interaction energy term 2cu is given as an instance of a complete union on the energy level of a spiritual wave c and a physical flow pulse u, or vice versa. The investigation and presentation of other such interaction effects will require care.

Hopefully, this whole endeavour will bring about a replacement of the present rather disengaged situation, with a cooperative endeavour to expand the factual knowledge on human nature.

.[See Appendix A: Outline of Compressible Fluid Flow Section 2.10 Wave Types and Stability].

Conclusions

The Ideal Gas Law, pv = const., occurs sequentially at the theoretical limit of the adiabatic equation series, pv^k = const., where the adiabatic index k becomes equal to + 1. and the equation becomes pv = const.. However, since this also requires that n, the associated number of degrees of freedom , or number of ‘microstates’, must become an infinity, then the ideal gas law is not physically possible, and evidently must exist only theoretically or only as a very useful approximation.

However, on the classical and pre-modern consensus that humans are a real composite of matter and spirit, body and soul, this infinity problem could conceivably vanish. This is because a valid exact thermodynamic human equation of state of format, pv = constant, could then emerge, with n equal to infinity, because of the postulated spiritual dynamism or intrinsically unquantified essence in human nature. This ideal, human exact equation of state would variously be thermodynamically entropic, isentropic or negentropic according to the particular human activity involved. [ It should be noted that the state equation refers to the human ‘body and soul’ interaction state and the human interaction entity, and not to a soul per se, or to a physical body as separate.]

The logic and evidence of the classical and pre-modern philosophical position on the nature of man as a spiritual/rational animal has always been overwhelming. The rise of our scientific and technological way of life, however, has routinely excluded spirit because of a requirement for scientific proof, which means experimental verification as well as logical theory. The proposed human equation of state theory predicts thermodynamic, dynamic and entropy effects which should be observable experimentally. The present hypothesis is therefore a scientific one.

In essence, our proposal is for the existence in humans of an ideal thermodynamic equation of state which would necessitate a dynamic capacity for numerical infinity. This equation, [pv = const.] and a second associated exotic, linear wave equation [p = −Av + B] , would govern such things as compression/rarefaction waves in human tissues, and would describe temperature changes and their associated entropy changes.

But, the existence of such an ideal equation of state in humans would also require an accompanying human spirit or soul because of the equation’s thermodynamic requirement for a physical infinity which could only be supplied by the intrinsically non-quantified dynamism of spirit or soul. Human mental and intellectual activity would necessarily generate unique thermodynamic entropy signals which would then be observable through associated characteristic brain/body temperature variations. This proposal is thus open to experimental examination and judgment, and so this argument for the reality of human spirit is canonically scientific.

Such thermodynamically described entropy/temperature signals should then relate to the data of neural signals and harmonic neural oscillations.

To the classical and pre-modern philosophical position on a soul/body human nature there may now be added a scientific theory i.e. one which is experimentally verifiable. The classical philosophical and theological position still holds on the weight of its rational argument, while the post modern, scientifically conditioned position of thought may now join the discussion on its own formal, scientific terms.

-----------------------------

The above Conclusions represent the completion of the First Step in this R&D project, namely the Proposal of a Human Equation of State designed to meet an expressed need in neurological science for a theory of brain temperature behaviour.

The Second Step is for its examination by neurologists for correspondence, or otherwise, of existing data with the proposed state equation. If this also is supportive, then an examination of Relevant Further Questions by neurologists and cognitive scientists could be made. If the fit of human data to predictions is close or unique, then the validation of the exact human equation of state would be established. In this case, the ‘body and soul ‘ theory of human nature already established from classical philosophy and theology would become scientifically supported as well.

---------------------------------

References

1. Power, Bernard A,, www.energycompressibility.info: Part VIII. Equations of State for Cosmic Fields. 2017.

2. …………………………………:Part VI: How Did Life Originate? The Role of Cell Waves and their Negative Entropy. 2016.

3. ………………………………… Part VII B What is Human Life? A Classical Viewpoint with a Verifiable Scientific Hypothesis. Nov. 2016.

4. Shapiro, A. S. The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 vols. John Wiley and Sons, New York, 1953.

5. Catechism of the Catholic Church: Section 365: Publications Service, Canadian Conference of Catholic Bishops, Ottawa, (Ontario) 1994.. [ “The unity of soul and body is so profound that one has to consider the soul to be the ‘ form ’of the body, that is, it is because of its spiritual soul that the body made of matter becomes a living human body; spirit and matter, in man, are not two natures united , but rather their union forms a single nature.”].

5a. Moreland, J.P., The Soul. Moody Publishers, 820 N. Lasalle Blvd., Chicago, Ill., 60610, 2014.

6. Beauregard, Mario and Vincent Paquette. “Neural correlation of a mystical experience in Carmelite Nuns” Neuroscience Letters, 405, 186-190 (2006).

7. Carhart-Harris, Robin L., R. Leech, P.J. Hellyer, M. Shanahan, A. Feilding, E. Tagliazucchi, D.R. Chivalo, D. Nutt “ The entropic brain: A Theory of conscious states informed by neuroimaging research data with psychedelic drugs”. Frontiers in Human Neuroscience. 03 Feb 2014.

8. Note: In a current Op Ed in the New York Times ( Int’nl Ed. June 5, 2018, pp 10-11) Prof. Stephen Asma wrote, on the irrationality of religion to him personally, but of its value as the unique soother of mangled human emotions. While both points are arguable, the second is evocative,

It brings to mind a marked characteristic of religion: For example, Inner Peace has been the hallmark of the Christian religion since its beginnings. St. Paul of Tarsus writes (in his Epistle to the Philippians 4:7): “……………the Peace of the Lord which surpasses all understanding”.

This peace experience was so universal that a standard liturgical greeting among Christians from those earliest days down to the present day was, and is : “May the Peace of the Lord be always with you”, with the reply: “And with your spirit”.

[‘Pax Domini sit semper vobiscum’; and ‘Et cum spiritu tuo’.]

This peace that Paul emphasizes was not seen as a soother of emotions in time of need, such as that which Prof Asma cites as a religious accompaniment. It was rather a spiritual state that was a simple fact accompanying acceptance of the new religious faith. Paul himself, an intellectual, could not ‘understand’ it. So it was clearly a state other than an ordinary mental notion, or any ordinary emotion; rather it was deeply immaterial, human and spiritual.

9. Lonergan, S.J., Bernard. Insight: A Study of Human Understanding. Philosophical Library Inc., New York, 1957.

---------------

‘To attain any assured knowledge about the soul is one of the most difficult things

in the world’……Aristotle

‘Man, the Rational Animal’……. …………Aristotle

“What is real is that which can be intellectually grasped and reasonably affirmed.”…Bernard Lonergan, S.J.

“ Insight is Joyous” ….. Richard Feynman

Human Ideal Equation of State

pv^k=1 = pv¹ = pv = C = RT

c_p / c_v = k = 1

n = 2/(k-1) = 2/0 = ∞

Copyright, Bernard A. Power,

February 2019

Back to Top

Appendix A

2.0 Outline of Compressible Fluid Flow

The following is a listing of some relevant basic compressible flow principles. For more complete treatment see texts on compressible fluid flow or gas dynamics.

2.1 Steady State Energy Equation

c² = c_o² − V²/n (1)

where c is the local wave speed, c_o is the static [i.e at V = 0] or maximum wave speed, V is the relative flow speed, n is the number of ways the energy of the flow system is divided (i. e. the number of degrees of freedom) of the system and [ n = 2/(k− 1), where k = c_p/c_v is the’ adiabatic constant’ or ratio of specific heats.]

Here, ‘relative’ means referred to any (arbitrarily) chosen physical flow boundary. The equation is for unit mass, that is, it pertains to ‘specific energy’ flow.

The case where V = c = c* is called the critical state. The ratio (V/c) is the Mach number M of the flow. The ratio (V/c_o) is also a quantum state variable. The maximum flow velocity V_max (when c = 0) is the escape speed to a vacuu:

V_max = √ n c_o.

2.2 Unsteady State Energy Equation

c² = c_o² – V²/n – 2/n (dφ/dt) (2a)

where φ is a velocity potential, and dφ/dx = u is a perturbation of the relative velocity. Therefore, in three dimensions, substituting V for u, we have dφ/dt = V (dx/dt) = Vc, and

c² = c_o² – V² /n − 2 (cV)/n (2b)

2.3 Lagrangian Energy Function L

L = (Kinetic energy) – (Potential energy) = ( c²+ V²/n) – c_o² , and so, from (2b)

L = − (2cV)/n (3)

2.4 Equation of State for Compressible, Ordinary Matter Systems

The equations of state link the thermodynamic quantities of pressure p, specific volume ( volume per unit mass v = 1/ρ] and temperature T. The basic equation of state for ordinary gases is the equilateral hyperbola of the Ideal Gas Law:

pv = RT ; p/ρ = RT = constant (4)

Equation 4 is seen to be isothermal (T= constant) . For adiabatic changes it becomes pv^k = constant, where the adiabatic constant k = c_p/c_v is the ratio of the specific heats at constant pressure and at constant volume, respectively.

Here, each point on the curve presents the values for a particular pressure and volume pair and shows how the two relate to each other when one or the other is changed. In this hyperbolic equation, the product of the two -- i.e. the pv- energy -- has a constant value as set out by the equation of state.

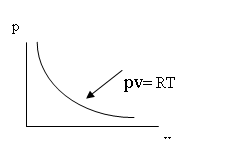
Hyperbolic Equation of State (Ideal Gas Law)

Equations of State can be formed for gases, liquids or solids. Here, we shall be concerned mainly with those for the highly compressible states i.e. for gases.

2.5 Waves and Flow

2.5.1 The Classical Wave Equation

∆²ψ = 1/c² [∂²ψ/∂t²] (5)

where ∆² = ∂²../∂x² + ∂²..^./∂y² + ∂²../∂z²; ψ is the wave amplitude, that is, it is the amplitude of a thermodynamic state variable such as the pressure p or the density ρ. The local wave speed is c.

The general solution of (5) is

ψ = φ₁ (x – ct) + φ₂ ( x+ ct) (6)

Equation 6 is a linear, approximate equation for the case of low-amplitude waves in which all small terms (squares, products of differentials, etc.) have been dropped.

The natural graphical representation of steady state compressible flows and their waves is on the (x,t), or space-time diagram.

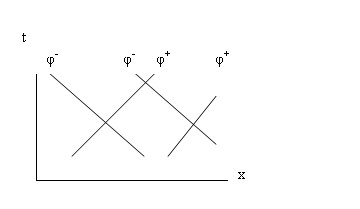
The classical wave equation corresponds to isentropic conditions. It represents a stable, low-amplitude wave disturbance, such as an acoustic–type wave.

Unsteady State ( Accelerating) Compressible Flow

In compressible flow theory, forces, when present, introduce a curvature of the characteristic lines for velocity on the space-time or xt-diagram. Space- time curvature thus indicates velocity acceleration and the presence of force .

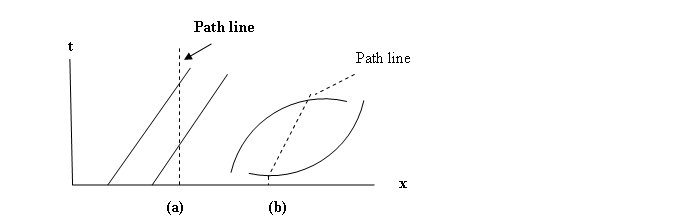
(a) Straight characteristics and path lines show steady flow and absence of force.

(b) Curved characteristics and path lines show acceleration and presence of force

In the case of compressible flow and 3-space (x,y,z) , a curved path line dx/dt = v (path) may be ‘transformed away’ to a straight line Lagrange representation [ dh/dt = 0].

[Note: In General Relativity the analogous distortion of its 4-space (x,y,z,t) to obtain a force- free representation is a tensor distortion.

However, it should be noted that general relativity is a continuous field theory, and, as such, excludes discontinuities or singularities such as shocks. Therefore, it appears to be fundamentally incompatible with quantum physics.

On the other hand, compressible flow as shown below in Section 3.1 on Visible Matter predicts shock discontinuities as the physical mechanism for the emergence of the elementary particles of matter by shock compression of an energy flow. Thus, compressible flow is compatible with quantum theory.

2.5.2 The Exact Wave Equation

Ѳ ψ = 1/c² ∂²ψ/∂t² [ 1 + Ñψ ]^{(k + 1)} (7)

where k, the adiabatic exponent, is k = c_p/c_v = ( n + 2) /n; and ( k + 1 ) = 2( n + 1)/n = 2(c_o/c*)². Here, pressure is a function of density only. This wave is isentropic, non-linear, unstable, and grows to a non-isentropic discontinuity called a shock wave.

2.5.3 Shock Waves

All finite amplitude, compressive waves are non-linear and grow in amplitude with time to form shock waves. These shocks are discontinuities in flow, across which the flow variables p, ρ, V, T and c change abruptly. (Note p = pressure, ρ = momentum).

2.5.3.1 Normal Shocks

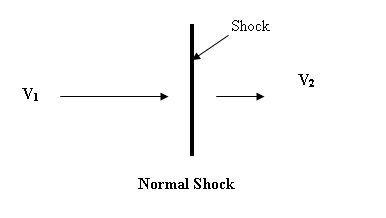
V₁ > V₂ (8)

p₁, ρ₁, T₁ < p₂, ρ_2, T₂ (9)

Entropy Change Across Shock:

∆S = S₁ – S₂ = − ln(ρ₀₂/ρ₀₁) (10)

Maximum Condensation Ratio:

ρ₁/ρ₂ = [n+1]^1/2 = V_max/c* (11)

2.5.3.2 Oblique Shocks

If the discontinuity is inclined at angle to the direction of the oncoming or upstream flow, the shock is called oblique.

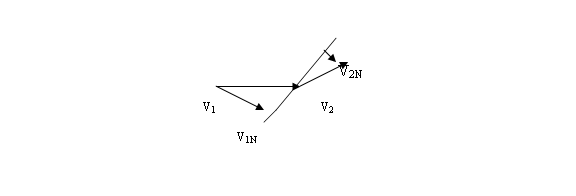
Oblique Shock

V_1N > V_2N

p₁ρ₁T₁ < p₂ρ₂

Since the flow V is purely relative to the oblique shock front, the shock may be transformed to a normal one by rotation of the coordinates, and the equations for the normal shock may then be used instead.

2.5.3.3 Strong and Weak Oblique Shock Options: The Shock Polar

For each inlet Mach number M₁ ( = V_N1/c), and turning angle of the flow θ, there are two physical options:

1) the strong shock ( intersection S) with strong compression ratio and large flow velocity reduction (p₂ >> p₁; V₂ << V₁, or

2) the weak shock (intersection W, with small pressure rise and small velocity reduction.

Which of the two options occurs depends on the boundary conditions: low back i.e. low downstream pressure favours the weak shock occurrence; high downstream pressure favours the strong shock.

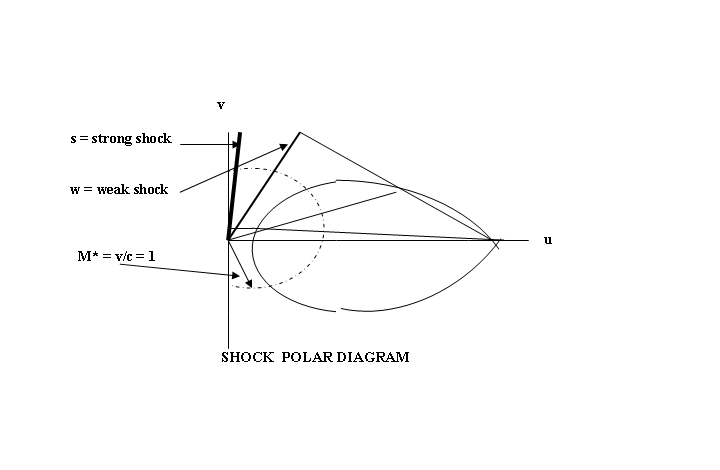
When the turning angle θ of the oncoming flow is zero, the strong shock becomes the normal or maximum strong shock, and the weak shock becomes an infinitesimal, low-amplitude, acoustic wave.

2.6 Types of Compressible Flow:

a) Steady, subcritical flow ( e.g. subsonic, V< c), governed by elliptic, non-linear, partial differential equations.

b) Steady, supercritical flow ( e.g. supersonic, V₁ > c) governed by hyperbolic, nonlinear, partial differential equations.

c) Unsteady flow (either subcritical or supercritical). These are wave equations governed by hyperbolic, non-linear, partial differential equations. They are often simplified to linear approximations, for example to the classical wave equation (5); if of finite amplitude they grow to shocks..

The solutions to the above hyperbolic equations are called characteristic solutions. If linear, they correspond to the eigenfunctions and eigenvalues of the linear solutions to the various wave equations of quantum mechanics ( Sect. 3.7), or, equally, to the diagonal solutions of the matrix equation of Heisenberg’s formulation of quantum mechanics.

2.7 Wave Speeds

c = [ c_o² – V²/n]^1/2 (steady flow) (12)

c = c_o² – V²/n – [(2/n)cV ]^1/2 (unsteady flow) (13)

c² = (dp/dρ)_s, [ c = (dp/dρ)_s^1/2] where s is an isentropic state.

Since V is relative, it may be arbitrarily set to zero to give a stationary or “local” coordinate system moving with the flow; this automatically puts c = c_o and transforms the variable wave speed to any other relatively moving coordinate system.

The shock speed U is always supercritical (U > c) with respect to the upstream or oncoming flow V₁.

2.8 Wave Speed Ratio c/c_o and The Isentropic Thermodynamic Ratios

c/c_o = [1 -1/n(V/c_o)²]^1/2 = (p/p_o)^1/(n+2) = (ρ/ρ_o)^1/n = (T/T_o)^1/2 (14)

All the basic thermodynamic parameters of a compressible isentropic flow are therefore specified by the wave speed ratio c/c_o. .

2.9 Relativity Effects in Compressible Flow: In compressible flows all velocities [V or u] are relative only, and, moreover, the wave speed c is a variable which is dependent on V and n; it decreases for larger velocities V. and it reaches its maximum value c_o at the static state i.e. at zero flow (V =0).

Interestingly, Equation (14)

c/c_o = [1 -1/n(V/c_o)²]^1/2 = (p/p_o)^1/(n+2) = (ρ/ρ_o)^1/n = (T/T_o)^1/2 (15)

shows that the correction factor for the effect of flow speed on wave speed c on the right hand side of the equation has the same form as the Lorentz Transformation of special relativity. If n = 1 the two correction factors become formally identical.

The differences from special relativity are that the wave speed c is now a variable and a function of the flow velocity V, and that there is the energy partition constant n. Since the wave speeds are low ( c = 334 m/s for air at m.s.l.), the ‘Lorentz’ corrections for physical compressible systems such as gases are relatively large. Also, the flow speeds can exceed the wave speed ( supersonic flow), whereas in special relativity theory, the wave speed c is a constant ( 3 x 10⁸ m/s) which can never be exceeded.

Photon shocks are thus impossible in special relativity, whereas in compressible flow they furnish a quantum physical theory for the origins of matter itself via the formation of the elementary particles of matter at compression shock discontinuities.

2.10 Wave Type and Stability

Compression waves are the rule in the baryonic physical world ( i..e. in Quadrant I on the pressure-volume diagram) Here, the usual equation of state is hyperbolic and its density waves are always compressive and all compression waves of finite amplitude grow towards shocks. Here, only acoustic compression waves ( i.e. infinitely low-amplitude compressions) are stable.

Rarefaction waves require an elliptical equation of state. Again these rarefactions only stable for acoustic infinitely low amplitudes. Finite amplitude grow to rarefaction shocks.

Stable waves of both rarefaction and/or compression and of finite amplitude are possible with the linear equation of state [ p = Av +B].

II

	+p
-v

+v

Equations of State for Various Wave Types

The criterion for wave behaviour is the curvature (d²p/dv² ) of the various isentropic equations of state:

1. If d²p/dv² is > 0 (i.e. the hyperbolic curve) compression waves form and steepen to form compression shocks, while rarefaction waves flatten and die out. Only compression waves of infinitely small amplitude (“acoustic” or “sound” waves” ) are stable. Compression shocks form from finite amplitude waves..

2. If d²p/dv² is < 0 , ( i.e. the elliptical curve) rarefaction waves form and steepen to form rarefaction shocks, while compression waves flatten and die out. Only rarefaction waves of infinitely low amplitude are stable.

3. If d²p/dv² = 0, (i.e. the linear state ) waves of either compression or rarefaction are stable, all amplitudes are supported and shocks are ruled out.

Copyright Bernard A. Power

February 2019

Back to Top