![]()
Section 4
Flow Acceleration and Centrifugal Force as a
Possible Cause of the Observed
Temperature Rise Anomaly in the Ranque-Hilsch Vortex Tube
Abstract In strong vortices small temperature rise anomalies are
observed. These are particularly evident and well studied in the so-called
Ranque-Hilsch Vortex Tube, but the
reason for the anomalies has been a matter of controversy. Here, we
present evidence that this effect is due to an increase in random vibratory kinetic molecular motion in the
radial dimension set up by imbalances in the strong centrifugal forces, thereby slightly raising the gas
temperature.
Contents

4.1 Introduction
4.2 The Ranque-Hilsch Vortex Tube
4.3
Previous Explanations for the Anomalous Temperature Rise Phenomenon
4.4 A
New Approach: Centrifugal Force in Vortex Flow
4.5 Vortex Flow
4.6 The Temperature Rise Anomaly in the Ranque-Hilsch Tube
4.7
Additional Atmospheric Observational Evidence for this Temperature Rise Anomaly
4.8 Conclusions
References

4.0 Introduction
Following observations on a rare whirlwind which occurs over cool
lakes in fine warm weather [1] we have,
since 2008, carried out laboratory studies
of various isentropic flow transformation models and devices with a view
(1) to understanding and controlling transformations of internal
pressure-volume energy into kinetic or flow energy, and eventually (2) into the
possibility of extracting this kinetic energy into useful work at better
efficiencies than with existing air motors such as turbo machines, jet engines,
vacuum machines and compressors..
Two laboratory models studied have been, first, isentropic nozzle
flow, both linear and swirled, and, second, the peculiar forced vortex called
the Ranque–Hilsch Tube [2,3].
Here we report some preliminary findings on the latter phenomenon,
 4.2 The Ranque-Hilsch Vortex
Tube
4.2 The Ranque-Hilsch Vortex
Tube
Ranque [2] invented and patented a
pressure or “push flow” vortex tube
consisting of a cylinder into which compressed air is injected tangentially to
form a gas vortex, having, typically, at one end of the cylindrical tube, an
axial exit port, and at the other end a peripheral exit annulus around a cone
valve. Astonishingly, while the axial
port emits cold air as might be expected, the annular port simultaneously emits
hot air. The total temperature spread can range up to 40 or 50 degrees C when
the inlet pressure is high and the tube radius is small. The same general
effect is observed with a so-called ‘uniflow’ model in which the cold and hot
exits are at the same end of the tube.

The Ranque-Hilsch tube is diagrammed in Figure 1. Typical inlet
operating air pressures are in the range of 1 to 6 atmospheres. Typical tube
sizes are from 5 cm in diameter, down to 1 or 2 centimeters for maximum
temperature separation.
Many detailed theoretical and experimental studies have been
carried out since Ranque’s discovery of the temperature separation
phenomenon in 1933, and subsequent findings and improvements by
Hilsch in 1946. However, while it
might be expected that gas exiting at an axial port would naturally be
colder than the inlet gas temperature because of isentropic expansion of the
compressed gas into the vortex core, the
accompanying exit of hot air at the other end of the tube has made the
phenomenon a matter of continuing
interest and controversy [2, 3,4,5,6}.
 4.3 Previous Explanations
for the Anomalous Temperature Rise Phenomenon
4.3 Previous Explanations
for the Anomalous Temperature Rise Phenomenon
Ranque [2] proposed that the observed cooling is due to adiabatic
expansion of the gas into the vortex core and that the heating is due to
adiabatic compression of the gas at the periphery or walls of the tube. Hilsch
[3] investigated the added the effects of internal fluid viscosity.
Later work [4,5,6] has investigated the effects of turbulence,
heat transfer processes, internal
secondary circulations and certain acoustic effects. Thus, the theoretical
explanations have become quite complex.
There was even some early speculation that the phenomenon might
involve a sort of “Maxwell’s Demon” effect in
which centrifugal forces might
somehow actually separate slow moving (
cold ) molecules from fast moving ( hot)
molecules. This approach was quickly
dismissed, as it involved a violation of the second law of thermodynamics.
Here, we adopt the basic original Rankine-combined vortex
models studied by Ranque and Hilsch, and then we analyze the effect of the very
strong centrifugal forces to provide a possible
new explanation for the anomalous heating – the general cooling is
considered to be already reasonably well
accounted for by adiabatic isentropic expansion of the air flowing from the
compressor into the vortex core.
 4.4 A New Approach: Centrifugal
Force in Vortex Flow
4.4 A New Approach: Centrifugal
Force in Vortex Flow
We
turn first to the centrifugal force which enters into linearly accelerated flow and in ‘curved’ accelerated flow, such as occurs in
a vortex.
The
centrifugal force Fc at any radius r of the vortex is given by
Fc= VT 2 /r
where VT is the tangential velocity.
Under
steady flow conditions, there is cyclostrophic balance in which, at any point, the centrifugal force
outward is balanced by the pressure gradient force acting radially inward:
Fc = VT 2 /r = −
1/ρ (dp/dr)
The centrifugal forces arising in atmospheric
vortices, such as in the cores of tornadoes, and even more so in intense laboratory vortices such as the Ranque-Hilsch
tube, are very large. We shall now
explore the possible role of these very large vortex forces in statistically
modifying the kinetic motions and energy partition of the molecules of the
compressible fluid itself so as to
produce the observed Ranque-Hilsch
tube temperature anomaly.
 4.5 Vortex Flow
4.5 Vortex Flow
In
a vortex, the gas or
fluid flow is roughly circular around
the central axis of rotation of the vortex
(Figure 2, below ), and the
necessary acceleration dV/dt arises from
the change in the direction of flow dV circulating around the vortex
core or axis, rather than from change in the magnitude of V as in the case of
linear flow accelerations.. Thus, because of the acceleration, the pressure
in the vortex decreases radially inwards towards the vortex core in both
compressible and incompressible flow..
There are two main types of vortex flow. First, there is the compressible potential vortex with ‘swirl’ or circulation
of the fluid around a central vortex
axis, but where the individual fluid elements themselves do not rotate.
Rather, their motion is analogous the motion of a compass needle when the compass itself is moved around in a circular
motion but the compass, needle does not
rotate on its own axis but always points
in the same direction even while the compass as a whole
‘circulates’.
In
a compressible potential vortex the relation between tangential velocity VT
and radial distance r from the centre is given by
VT r
= Γ =constant
which is just a statement of
the conservation of angular momentum Vr,
where Γ with dimensions of angular momentum is called the circulation,
and VT is the tangential
velocity at any point of radius r.
The potential vortex
is so-called, because its motion can also be described by a potential velocity function φ, such
that dφ/dx = V. It is also often called a free
vortex [7,8, 9,10].
The second main type of
vortex motion is solid or wheel-like rotation, sometimes called a forced vortex
or rectilinear vortex, which is
described mathematically as
V T/r = ω
were ω is the rotation
with the dimensions of frequency (radians per second).
Natural atmospheric vortices
such as tornadoes, waterspouts and dust devils are often modeled as a
combination of these two vortex motions, that is, with an outer potential fluid motion and an inner core in solid
rotation. [ 8, 9,10, 11 ].This combination is called a Rankine combined vortex, or
simply a Rankine vortex.(Fig. 2).
For the radial pressure
profile in a Rankine vortex, we have, [10 ] the following relationships;
(a) In the outer potential vortex :
p = po
−( ρΓ2 / 4π2) ∫dr/r3
= ρΓ2/ 8 π2
r2
(b) In the inner forced
vortex or core:
p = po
[ρΓ2 (r1 2 – r2 ) / 8 π2 r14
]
The combined pressure profile
across the Rankine vortex is shown in
fig. 2 below.
-p
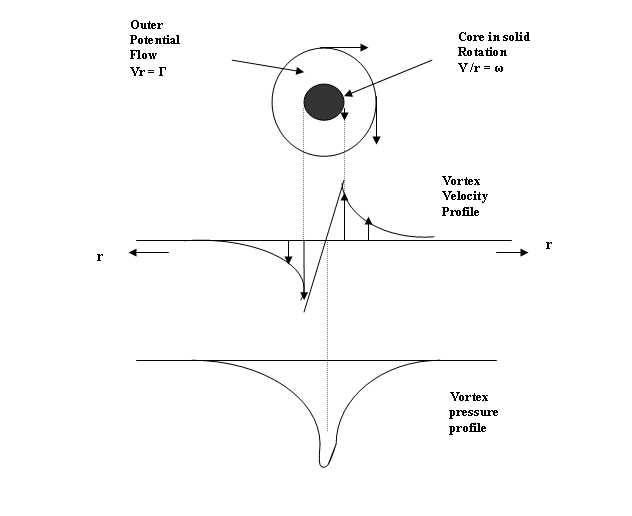
Figure 2.
Radial Profiles of Tangential Velocity and Pressure in a
Rankine-combined Vortex
It is worth
noting that there is an important difference is the relationship of velocity to
the radius in a vortex versus that in the Equation of Continuity. In a vortex,
the velocity V is proportional to 1/r; but in the Equation of Continuity (
ρVA = constant) the velocity is
proportional to 1/r2. We
shall have occasion to make use of this difference shortly.

4.6
The Temperature Rise Anomaly in the Ranque-Hilsch Tube
We shall use this basic
Rankine-combined vortex model to describe the operation of the Ranque- Hilsch
tube, and then propose some modifications to it that we feel are required by the enormous centrifugal forces generated
by high flow velocities and small radius of the vortex tube.
We now consider the equation relating average specific molecular
energy ( c2 ) i.e. sound
speed energy, to internal pressure volume energy in the ideal gas law:
c 2 = k pv = k RT
Here, k, the ratio of
specific heats cp/cv , is also related
to the number of degrees of energy partition n as
k = (n+2) /n = cp/cv
Thus, for n equal to 5 as in air, k equals 1.4. Therefore, if n were to increase from 5 to 6 with a gain of
one whole degree of freedom, k decreases to 1.33 . Then both c2 and the gas
temperature T must increase by the factor 1.4/1.33 = 1.05. Therefore at
a base temperature of 293 K this would mean a rise of 14.6 C in the air
temperature from the action of the
centrifugal force.
Of course, at small tangential velocities and consequently small
centrifugal forces, the effect on the motion of the gas molecules will be less,
and only some fraction of a degree of freedom change would be expected, giving
a smaller temperature rise.
If we were to express the relative centrifugal force strength in a
vortex by the Mach V/c, at a base temperature of 293C we could calculate the
temperature rise as
+ ΔT
= [M x 1/6] /5] x 293˚C
with the results shown in Table 1.
Table
1
Temperature
Rise Anomaly Due to Vortex Centrifugal
Force
Maximum Mach
Number Portion of Molecules Temperature Rise + ΔT
Tangential Velocity [ M x 1/6]
/5 [ M x 1/6] /5] x 293˚C
(m/s)
30 0.09 0.003 0.9˚ C
40 0.12 0.004 1.2
50 0.15 0.005 1.5
60 0.19 0.006 1.9
70 0.22 0.007 2.1
80 0.25 0.008 2.4
90
0.29 0.01 2.8
100 0.32 0.011 3.1
300 1.00 0.033 9.8
These temperature rises are in the same general range as those
observed in the Ranque-Hilsch tube experiments.
We must naturally now address a further relevant key question :
What possible physical mechanism might introduce such a postulated additional
degree of energy partition into the vortex?
As we have pointed out, in a vortex there is cyclostrophic balance between the pressure gradient force directed
radially inward and the centrifugal force directed radially outward.
Fc =
Vt2 /r = − 1/ρ (dp/dr)
However, it would be unreasonable to expect a perfect and
continuous balance between these opposing forces in any real flow, and so we
may reasonably expect that there will be substantial vibratory oscillations set
up as the cyclostrophic balance is momentarily disturbed and then restored
.
We now propose that the
vibratory oscillations in the vortex flow will constitute an additional
source of energy partition, so that the value of n, ( in air for example ) will tend
to increase from 5 towards the value of
6. The values set out in Table 1 above would
then apply and this mechanism would provide an explanation for the observed
temperature increase in strong vortex flows such as the Ranque-Hilsch Tube.
Of course, the above formulation of the proof is preliminary; it
can undoubtedly be made more quantitative and rigorous, but the essential
proposed process should be clear, and
appears to be supported by the
preliminary results.. There can be either one or two outlet ports or nozzles as described earlier. The temperature and pressure changes are
quasi-isentropic.
The expansion of the pressurized inflowing air in the tube takes place in two ways: (a)
by the usual isentropic expansion in the
duct with the pressure drop ( and
cooling) determined by the ratio of
inlet orifice area to outlet orifice or nozzle area and (b) the additional expansion ( and cooling)
which takes place in the superimposed
vortex because of the accelerated
or curved flow.
To repeat, the new proposed
flow effect which may help explain the anomalous temperature rise in the R-H Tube
is that the very high centrifugal forces induced in some portions of
the flow introduce vibratory motions
which constitute an additional degree of
energy partition and hence are a main
cause of the temperature rise anomalies that are
observed the tube flow.
[Another possible xplanation
is that the centrifugal force suppresses the
small scale turbulence in the flow and converts it into molecular vibrations
or heat motion and so that this accounts for he heat rise.[ Check this thought.
(Insert May 16/11) : Usual explanation of the Ranque-Hilsch effect
is via conservation of angular momentum, etc,
Here we seek an explanation at the energy level. The internal energy
given by the sound speed mc2
= m pv = mRT involves the temperature T via the 5 degrees of freedom of random motions of the
gas. However, there is also the linear flow aspect where the isentropic
relationship predict the temperature dependence on the flow velocity.
We now consider the
additional energy (kinetic) in the
random small scale turbulence which is suppressed by the centrifugal force of
the vortex circular motion. And we attempt to quantify its effect on the
observed temperatures.
We know that streamline
flow velocity affects the temperature via the isentropic relationships. So why
would not small scale random turbulence packets of kineticc energy not also
affect the temperature when theeeeey arise and disappear?. We know that if
turbulence sets in in a previously smooth linear flow there is a pressure rise
and so also a temperature rise. So, a linear velocity drop is a temperature
rise. Q. Is then a random velocity drop ( i.e
turbulence suppression) also a
temperature rise ( as observed in the R-H effect.?

4.7 Additional Atmospheric Observational Evidence for the Temperature
Rise Anomaly
Because of the flight hazard from swirling airborne debris in
land-based tornadoes, detailed aircraft temperature profiles through them are
not available. However, waterspouts, even severe ones, are relatively
debris-free, and they can be penetrated with suitable aircraft, so that data
from a series of waterspout temperature and pressure soundings are available
[12,13,14].
Golden [12] found that
waterspouts typically have temperature profiles which show an unusual
temperature rise anomaly in an annular
zone of about +3 degrees at
moderate levels above the sea surface. C.
Later work with an aerobatic aircraft showed a smaller temperature rise
of 0.3 ˚C near the core near the
cloud base [13,14].
The cause of this
waterspout temperature rise anomaly has apparently not been analyzed in detail,
and it is ordinarily ascribed to some
such effect as compression and warming of subsiding air in the vortex Now, however, we suggest that it is, in fact,
caused by the same basic phenomenon
producing the ( much larger ) temperature rises which occur in the
Ranque-Hilsch tube, and that it is therefore
to be explained as a result of an energy transformation involving an
increase in internal kinetic vibratory motion arising from oscillations or
vibrations in the imperfect cyclostrophic balance of the strong centrifugal and pressure gradient forces in
the vortex..
 4.8
Conclusions
4.8
Conclusions
We have outlined the effect of very strong centrifugal force in
vortices acting to distort the average
kinetic speed of molecules in a flow of fluid, and thus of slightly raising the average temperature in the
affected annular ring of the vortex. This we propose is the explanation for the
observed temperature rise anomaly in the Ranque-Hilsch tube. Such a temperature rise anomaly is also
observed in atmospheric waterspouts;
presumably it also exists in tornados where the centrifugal forces are
even stronger.
Many peculiarities remain to be studied in the Ranque-Hilsch tube
vortex. Hopefully, the present proposed solution to the problem of the temperature rise anomaly may
assist in their solution.
References
1. Power, Bernard A., Tornado-genesis
by an Isentropic Energy Transformation. http//www.energycompressibility.info
2008.
2. Ranque, G. J., Experiences sur la detente giratoire avec
production simultanee d’un echappement d’air chaud et d’un echappement froid. J. de Physique et de Radium, 4, h112-114, 1933.
3. Hilsch, R.
The Use of expansion of gases in a centrifugal field as a cooling
process. Review of Scientific
Instruments, 18, 2 108-113, 1947.
4. Gao, Chengming. Experimental Study on the
Ranque-Hilsch vortex tube. Doctoral thesis.
Technische Universitet
5. Albhorn, B, and
6. Colgate, S. A., Vortex Gas Accelerator. AIAA
J., 2, No. 12, 2138-214.1964.
7. A. H. Shapiro, The Dynamics and Thermodynamics of
Compressible Fluid Flow. 2 Vols.
John Wiley & Sons,
8.. Brunt, David, Physical and Dynamical Meteorology.
9. Lamb, Sir Horace. Hydrodynamics. Dover Publications Inc.,
10.
Prandtl, L. and O. G. Tietjens, Applied
Hydro- and Aeromechanics, Dover
Publications Inc., New York, 1957.
11.
Rankine, W. J., A Manual of Applied Mechanics, Charles
Griffin,
12. Golden, Joseph H., The Life Cycle of Florida Keys’
Waterspouts: I. J. Appl. Meteorology , pp 676-692, Vol 13, No. 6, Sept. 1974.
13. Golden, Joseph, H, and
Howard B. Bluestein, “A Review of Tornado Observations”. In . The Tornado: Its Structure, Dynamics,
Prediction and Hazards. Church, C., Burgess, D., Doswell, C., Davies-Jones,
R., (eds.). AGU Monograph 79, pp. 319-352, American
Geophysical
14. Leverson,
V.H., P.C. Sinclair and J.H. Golden. “Waterspout wind, temperature and pressure
structure deduced from aircraft
measurements .” Mon. Weather Rev. 105, 725-733, 1977.
15.
Standard Handbook for Mechanical
Engineers, Sect. 9-8 to-9-13 by E. N. Fales, T. Baumeister and L.S. Marks,
Editors. McGraw-Hill Book Company,
16. Also see http://www.reuk.co.uk/Betz-Limit.htm
![]() Copyright: Bernard A. Power 2009
Copyright: Bernard A. Power 2009
Section Links:
Section 1: Linear ( streamline) Flow and Flow Power
Amplification
Section 2: Invention
No.1: A New Isentropic Air Motor and
Clean Energy Source
Section 3: To be
posted in near future
Section 5: A Note on Isentropic flow ‘ Perpetual Motion’