Tornado Structure, Intensity Limits and Intensity Prediction

( May 2013)

Index

Summary

Part 1: Tornado Structure and Wind Speed

1.0 Introduction: The transformation of atmospheric internal energy into tornado wind speed

1.1 Rare miniature whirlwind occurring in warm, clear weather over a calm, cool lake

1.2 The structure of this strange, tiny whirlwind. Reasons why it is not a heat engine

1.3 An alternative explanation: The mini-vortex flow involves an isentropic speed-up

1.4 A tentative sequence of events for the evolution of the mini-vortex

Conclusions: Part I

Part 2. Tornado Dynamics , Intensity Limits and Intensity Prediction

2.1 Vortex features in general

2.2 Vortex motions: The Rankine Combined Vortex

2.3 The source of the rotation needed in the vortex core

2.4 The driving pressure difference and ‘throughflow’ or mass flow rate of the tornado

2.5 Other types of tornado- like vortices

2.6 Satellite vortices, ‘sub- vortices’ or ‘suction’ vortices

2.7 Summary of the main tornado features.

2.8 A method of estimating tornado wind intensity limits from air mass humidity

2.9 A unifying vortex element: The Flow Condensation Discontinuity

3.0 Conclusions

Summary

Tornados are the most violent wind storms known, sometimes reaching wind speeds of around 250 to 300 mph. ( 112 to 134 m/s) [1]. However, there seems to be no compelling theoretical reason why they shouldn’t continue to increase in speed right up to the sonic speed of around 700 mph. ( 313 m/s). Fortunately for us, they don’t. So the question arises: What limits tornado wind intensity to less than 300 mph?

Tornadoes usually are accompanied by, or grow out of, violent thunderstorm clouds whose complexity makes it very difficult to know where to start for an adequate understanding of their structure and mechanism. In addition, tornadoes are seemingly a composite of two different types of air flows having different flow properties--- a small central core of rotating fluid is smoothly surrounded by a much larger area of circulating but non-rotating fluid, yet all the while the tornado somehow maintains a unified continuous flow system through the two different types of air flow, from inflow at ground level to outflow in the parent storm cloud above. It is quite puzzling.

However, a fortuitous observation of a very simple, rare, mini- vortex over a calm, cool lake in fine weather in Mont Tremblant Provincial Park, north of Montreal, points to one unexpected feature, namely that the high vortex swirl velocities are apparently produced by only small temperature changes of a few degrees in an adiabatic/isentropic vortex inflow process, rather than by the inefficient heat engine process sometimes proposed, and this conclusion should apply to full scale tornadoes as well.

Three new insights will be the subject of this Website. The first is that the main speed-up process in a tornado may be a clear air, isentropic/adiabatic transformation, in which a small amount of the internal heat of the air flow is transformed into the observed high vortex wind speed. Second, this high speed- up, isentropic flow process is terminated by the formation of the tornado funnel cloud which releases latent heat of condensation into the vortex as it forms and thereby stops the high speed- up, isentropic phase completely and allows a heat engine process to take over. This presents the possibility of predicting the general level of tornado intensity on a given day from the relative humidity of the air masses involved. Third , this same condensation discontinuity in the flow also introduces fluid rotation directly into the core where it is needed to stabilize the vortex.

We should note that an enormous amount of data and theoretical insight already exists on tornado structure and dynamics, and that the new insights offered here must be evaluated within the framework of this existing knowledge.

Part 1: Tornado Structure and Wind Speed

1.0 Introduction: The Transformation of Atmospheric Internal Energy into Tornado Wind Speed

As background to these energy transformations, and apart from the straight line winds of ordinary weather systems, there are two principal atmospheric physical processes that can cause the observed, localized air flow speed up by flow expansion into the low pressure core of vortices or whirlwinds.

First, there is the heat engine process in which heat energy difference-- that is to say, either internal heat or heat arising from temperature differences between adjacent atmospheric air parcels -- is converted to kinetic energy of wind flow, ½ mV² , by a volume expansion of low efficiency,with accompanying small flow speed increase.

Second, there is the isentropic conversion of internal heat energy into flow speed via a linear flow expansion which, under the action of some physical constraint to the flow, converts internal heat energy and small, commonly occurring, temperature and pressure differences, to large flow velocities. [In ordinary linear flow, such a constraint could be the walls of a converging/diverging nozzle; in free flow in the atmosphere, the constraint is the centrifugal force acting on the curved air flow in a vortex and especially on the walls of the funnel of a vortex].

1. The heat engine equation [7] is as follows:

V = [ 2 c_p ΔT (ΔT/T_o) ]^1/2 (1)

For example, a 1˚C temperature drop in the warm air flowing into a vortex in the heat engine process increases the flow speed V by 3.6 m/s.( 8 mph) [ V = [2 x 1004.6 x 1 x 1/303]^1/2 = 3.6 m/s]. See Table 1, Sect. 1.3. The prevailing temperature is taken here as 303˚ K (30˚ C) and c_p is the specific heat of air at constant pressure

2. The second possible process is the isentropic/adiabatic flow speed-up transformation [2, 11, 22] whose equation, linking flow velocity to expansion temperature change, is:

V = n^1/2 c_o [1 − T/T_o]^1/2 = n^1/2 c_o [ ΔT/T_o]^1/2 (2)

In this isentropic transformation ( Table 1, Sect. 1.3) the same 1 degree C temperature drop in the vortex inflow will yield a wind speed increase of 43 m/s (96 mph), or 12 times as great as that of the heat engine process! [V = 5^1/2 x 334 x [1/303]^1/2 = 43 m/s] . In this example, n , the energy partition number, is 5 for air, c_o is the local speed of sound taken as 334 m/s, and the background air temperature is taken as 303˚ K.

[Put another way equivalent way, we could also say that : A small local pressure differential of 11 millibars (1100 Pascals) between two points in an air mass which is suitably restrained laterally by the centrifugal force of a swirl, could cause an isentropic flow expansion and produce a tangential flow velocity of 43 m/s and a temperature drop in the air of 1 degree C. ]

ere n = 5Heremm

Our relevant question now is: Do these processes also act in tornadoes, and can they explain the observed tornado wind speeds and behaviour?

Fortunately, a chance, first -hand observation in 1987 of a rare, fine weather, mini-whirlwind in the air just above the surface of a small lake in Parc Mont Tremblant north of Montreal, furnished a very simple meteorological situation to analyze which has yielded an answer to our questions.

The winds in the violent little mini-whirlwind, which lasted about 15 seconds, were estimated to be 30 - 35 m/s (67 -78 mph). The column of swirling cloud or mist was about 1.5 meter in diameter by about 2-3 meters high. The maximum temperature difference between lake water and the air over it was about 5˚C. The weather that day was fine, the sky was cloudless and the wind over the lake surface elsewhere was almost calm.

The conclusion of the analysis was that the brief, swirling wind speeds of about 35 m/s in the tiny whirlwind could only be explained by an isentropic conversion of 0.5 - 1 degree C of the temperature difference between the air at the lake surface and the air 6 to 8 feet above it, into wind speed, since this process yields the observed winds of 35m/s, whereas the heat engine process would produce winds of only about 3.6 m/s.

In the years since 1987, much effort has been put into applying these insights to laboratory flow devices, to the theoretical structure of full size tornadoes in the atmosphere, and to the apparent limitation of their wind speeds to around 135 m/s ( 300 mph).

These insights have now led to a new general insight into tornado structure, and to a new approach to the prediction of tornado intensity limits.

To sum up, most intense tornadoes in the United States have maximum wind speeds of less than about 90 m/s (200 mph). The expected upper limit in wind speed is usually considered to be about 130-140 m/s 290 – 316 mph) [1].

However, since it is relatively easy in the laboratory to accelerate an air flow up to the sonic limit of 313 m/s ( 700 mph) --- for example, in a converging- diverging nozzle flow) [2, 11] --- one may wonder why tornado winds are usually held down to only about 90 m/s (200 mph) or so.

An understanding of this apparent tornado wind speed limit would have important practical consequences for structural engineering, building design, insurance risk calculations, public safety and so on.

Full scale tornados are very complex dynamic systems; they occur associated with intense convective storm systems and the extreme violence of their wind and weather make the gathering of precise observational data about them a matter of difficulty and danger. Years of intense work have yielded a great understanding of much of their nature [1]. Yet many points are still a matter of debate. Consequently, any new data or insights into their nature are very desirable.

Doswell and Burgess have stated [3] that: “From a purely dynamical viewpoint, tornadoes arise from amplification of either existing or locally produced vorticity. However, this is a somewhat abstract framework for understanding tornadoes”. And so they go on, instead, to discuss them from the practical standpoint of the convective features of tornado storm cloud systems.

Here, we shall concentrate on the physical process of the conversion of internal heat energy of the air masses to isentropic flow expansion, with its associated small temperature drop and large flow speed- up, and its application to full-scale tornadoes in the atmosphere.

1.1 Rare miniature whirlwinds occurring in warm clear weather on calm, cool lakes

These very rare, mysterious, fine weather, tiny but violent whirlwinds first came vividly to personal attention of the Website author, a professional meteorologist, on Sept. 2, 1987, during a fishing expedition in Mont Tremblant Provincial Park north of Montreal, Quebec. My late wife, Pauline, and I were in a small rowboat on Lac de la Fourche, a small body of water, about a third of a mile long by half that distance wide.

It was a fine, warm sunny morning with little or no wind. At about 11 a.m. Pauline called out in alarm at the sudden appearance out of nowhere of a small, violently whirling, column of mist over the water in a small bay about 100 meters from our boat and about 50 meters from the forested shoreline.

The swirling mist column was about 2 to 3 meters feet high and 1.5 meters in diameter, centered over a circular patch of somewhat ruffled surface water about 8 meters in diameter. The central mist column was whirling round and round violently, all the while emitting a hissing sound. After about 15 seconds in the same location, the whirlwind disappeared as suddenly as it had formed, leaving only a small, darkened, breeze- ruffled area on the surface of the water which then drifted away across the lake at about 10 km/hr toward the eastern shore. This lake is shallow, not over 7 meters or so deep at the deepest spot.

An inspection of the little bay along the north shore of the lake where the whirlwind had erupted showed no signs of any disturbance in the water itself, which was perfectly clear right down a meter or so to the undisturbed lake bottom. Obviously the whirl had been in the air above the water only. The lake water temperature was cool at around 18 ˚C. The air temperature was warm at about 25˚C ( 24 to 26˚C). This situation, with cool air at the surface and warmer air above is just the reverse of the temperature stratification that occurs in tornados, waterspouts and dust devils where the air is warm at the surface and cooler aloft. This strange set of circumstances, almost completely the opposite of conditions in storm tornadoes, naturally provoked intense curiosity. It certainly invited careful study and analysis, especially since the weather conditions were of extreme simplicity. The violent little whirlwind with winds estimated at 30-35 m/s ( 67 to 78 mph) had apparently emerged suddenly ‘out of nowhere’! How could this happen?

Further investigation soon showed that there was only one other account in the scientific literature of a similar phenomena occurring in North America. That one reported a whirl of spray “the size of a flour barrel” suddenly appearing on a small lake in the Adirondack Mountains, New York State, on a fine sunny day in May 1920 [4]. It gave off a “splashing” sound and lasted a minute or so. In Europe there were reports of a couple of somewhat similar occurrences [ 5 ].

We later met with M. Bernard Bruneau, Park Warden of Mont Tremblant Provincial Park for 24 years, who told us that he also had seen such tiny whirlwinds on the Park’s lakes, but only on two or three occasions during his entire career, and once on a calm stretch of a small river. All had occurred on fine, sunny, warm, nearly windless days in late morning or shortly after noon.

Clearly, what we had seen was a very rare event. The weather at the time, also, was so simple, meteorologically speaking, compared to tornadoes and waterspouts, that it invited close scientific analysis [6]. The general situation is shown in Figures 1,2,3.

Fig. 1. Watercolour sketch of small, rare whirlwind seen on Lac de la Fourche, Parc Mont Tremblant, Quebec on Sept. 2, 1987. ( Sketch by B. Power)

18˚ 23˚ 25˚

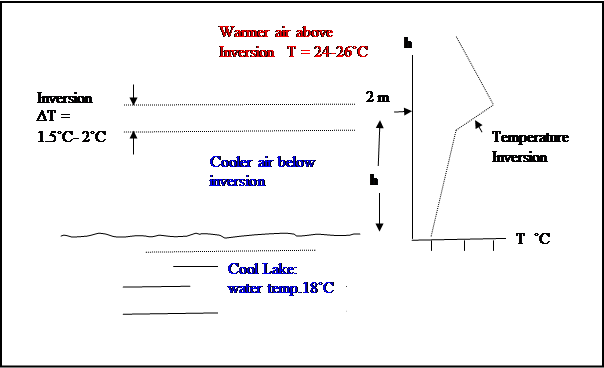
Figure 2. Estimated Temperature profile over cool lake surface

Cool water temp. 18˚C

Fig. 3 Schematic cross section ( a) Incipient whirlwind (b) The fully formed vortex.

1.2 The structure of this strange, tiny whirlwind: Reasons why it was not a heat engine

The first conclusion of the initial study [6] was that, if the vortex and its strong swirling winds were an atmospheric heat engine, then the heat source must be the warm air just above the temperature inversion at a height of about two meters above the surface of the lake.

Indeed, it has in the past been one explanation of tornados that they are atmospheric heat engines, driven by convective instability between a warm moist source at the ground level and the upper atmospheres at much cooler sink temperatures, the general temperature differential in a mature tornado thus being about 40 - 50° C. The heat engine [ 7] is an irreversible, non-isentropic flow, where the relationship between velocity V, and thermodynamic quantities of heat Q, and temperature T, is given [6,7] by:

V = [ 2 c_p ΔT (ΔT/T_o) ]^1/2 (1)

where c_p is the specific heat at constant pressure ( 0.24 gram calories in air at 20C or 1004.6 J/kg), ΔT = T_o − T_i is the temperature drop from source to sink, and ΔT/T_o = ( T_o − T)/T_o = 1 − T/T_o is the thermodynamic efficiency of the heat engine as required by the 2^nd law of thermodynamics, which limits the amount of work that can be extracted from any given heat input. (The work done ( dW = pdv) enters through the expansion of the air as it flows into the lower pressure of the vortex core ).

Now in the case of the mini-whirlwind, observed in 1987, the heat difference ΔT between the heat source in the warm air above the inversion over the lake and the heat sink in the core of the vortex at the lake surface could not be more than the temperature difference between water temperature and air temperature which was at most about 7˚C, and more likely was on average less than half that value, 3.5˚C.

In that case, the resulting winds from Equation 1 for a heat engine operating at a ΔT of 3.5 degrees would be only about 9 m/s, far below the 30 to 35 m/s observed. We cannot therefore explain this cool-lake whirlwind as a heat engine transforming heat energy into wind speed, that is, by transforming potential energy of heat into kinetic energy of wind speed. It appeared that some other mechanism to explain the high swirling wind speeds must be sought.

1.3 An Alternative Explanation: The Mini-vortex Flow Involves an Isentropic Speed-up

Turning from the heat engine model, we next examined the isentropic/adiabatic flow expansion [22] and its accompanying transformation of internal heat energy ΔQ into kinetic energy ( ½ mV²) and flow velocity V. Since the expansion transformation is isentropic, the heat transformation is wholly internal, no heat is passed to or from the environment and much large flow velocities emerge.

These isentropic transformations of internal energy into flow velocity, with no heat flow into or out of the system, are given by [2,11] the following equation:

V = n^1/2 c_o [1 − T/T_o]^1/2 = n^1/2 c_o [ ΔT/T_o]^1/2 (2)

.

This is derived as follows: We start with the energy equation in terms of actual wave speed c, static wave speed c_o, temperature T, flow velocity V, and n, the number of ways the energy of the air is divided. ( n also equals 2/ (k − 1) where k is the ratio of specific heats c_p/c_v, and has the value of 1.4 for air.) As is usual in flow theory, we consider unit mass of fluid, so that m (= 1) does not appear explicitly in the energy equation which is as follows:

c² = c_o² − V² /n

c²/c_o² = 1 − V² / nc_o²

If we now further restrict the adiabatic case to reversible flow, we have the convenient isentropic relations [10]

c²/c_o² =( p/po)^2/n+2 = ( ρ/ ρ_o)^2/n = T/T_o and so

T/T_o = 1 − V² /n c_o² _,, whence we have Eqn. 2 above, i.e.

V = n^1/2 c_o [1 − T/T_o]^1/2 = n^1/2 c_o [ ΔT/T_o]^1/2 (3)

which gives the relationship between increased flow velocity V and ΔT, the temperature drop during the isentropic expansion.

Table 4 gives the computed values of V for a range of temperature changes ΔT, calculated from Equation 2, taking n = 5, c_o = 334 m/s, and To = 303˚K ( 30˚C).

Table 1

Flow Velocity Versus Temperature Change (a) in a Heat Engine and (b) in Isentropic (adiabatic, reversible) Expansion of Air Flow

C_p = 1004.64 = 0.24 x 4186 J/kg/deg C
T_o = 303 deg K (30˚ C) Heat Engine Process Isentropic Process

c_o = 334 m/s Velocity Increase (m/s and mph) Velocity Increase (m/s and mph)

ΔT T_o T₁ V = [ 2 c_p ΔT ( 1 – T_o/T₁)]^1/2 V = n^1/2 c_o [ 1 – T₁/T_o]^1/2

m/s mph m/s mph

0.5˚ 303K 302.5˚K 1.29 2.9 30.3 67.9

1 “ 302˚ 2.58 5.76 42.9 96.0

2 “ 301 5.15 11.5 60.7 135.7

3 “ 300 7.73 17.3 74.3 166.2

3.5 “ 299.5 9.03 20.2 80.2 179.4

4 “ 299 10.3 23.0 85.8 192

5 298 12.9 28.8 95.9 214.6

10 “ 293 25.8 57.6 135.6 303.4

Note 1: Values in blue are for the observed cool lake vortex wind speeds corresponding to various possible temperature drops

2. Conversion factor: m/s x 2.237 = mph

It is apparent that isentropic flow velocity transformations can easily account for the magnitude of the winds in this tiny, intense vortex ( 35 m/s) as arising from the available temperature differences (1 to 3 degC) that exist in the inversion over the cool lake surface. Table 4 shows that even a temperature differential at the inversion level of only 0.5˚C transforms or corresponds to a flow velocity of 30 m/s or 68.1mph, while a 1˚C temperature differential could produce a wind speed of 43 m/s (96mph).

Therefore we can now apparently relate the Lac de la Fourche observed wind speeds of 30 to 35 m/s to a small temperature difference of only about 0.5 to 1˚ C in the temperature inversion over the lake by invoking an isentropic energy transformation.

If this mechanism acts in one vortex in the atmosphere, it ought to be able to act at other similar atmospheric vortices large or small, and so we may also have an explanation that should be relevant to tornados and waterspouts as well. The isentropic expansion transformation of internal heat energy corresponding to a flow’s temperature drop of only 1 to 3 ˚ C--- a commonplace occurrence in the atmosphere-- will account for the maximum observed wind speeds in most tornadoes (Table 1). 42.9 m/s -74.3 m/s ( 96 to 166 mph0. A difference of 5˚ C, upon isentropic flow expansion would give 95.9 m/s (214 mph) equivalent to most intense tornadoes.

We have shown that the isentropic transformation of temperature to flow velocity can explain the intensity of the observed winds in the mini-vortex over the cool lake and that the heat engine process can not. We therefore reasonably have concluded that the actual process at work is the isentropic one.

But, we have not examined the precise physical reasons why this should be so. We shall not attempt to do this here in a detailed or rigorous way. But, we point out the effect of centrifugal force and acceleration generated by the swirling circular flow.

For example, in the linear flow of air through a converging nozzle [2,] the air accelerates isentropically because of the reduction in cross sectional area of the nozzle. Put another way, if the air motions are restricted in two directions - say, the x and y directions - the flow must accelerate in the flow or z- direction in order to conserve the mass flow constancy under a fixed driving pressure differential.

In the case of a flow in a vortex, the centrifugal force set up by the circulation and/or rotation plays the part of the solid wall of the converging duct of the nozzle; it acts to restrain the direction of expansion and to permit an acceleration in the unrestrained direction, which is now in the tangential flow direction.

This centrifugal force effect acts in both the isentropic and the heat engine cases, since the air flows in circular motion in both cases, but with different velocity increases--- large in the isentropic case and much smaller in the heat engine case.

Note. While we have looked at this isentropic flow process as a transformation of internal heat into flow speed increase and temperature drop by linear expansion, we could just as validly have presented it as a conversion of pressure differences to flow speed, since from the isentropic equations above, we have

ΔT = T_o [ V² /nc_o²] and Δp = p_o [ 1 – (T/T_0‑)^n+2/n ] = p_o [ 1 - (V²/nc_o²)^n+2/n ]

which links pressure differences Δp to temperature differences ΔT and isentropic flow velocity V.

1.4 A tentative sequence of events for the evolution of the mini-vortex.

The available data on this mini-vortex suggest that the possible life cycle evolution is somewhat as follows:

1. With warm air from the land draining out on top of the shallow layer of cool air over the lake surface in the early morning, a temperature inversion forms and persists from shortly after dawn until mid - morning. (Figure 4 (A and C)).This inversion is topped at about 6 to 10 feet above the lake surface.

2. Late morning of a calm, sunny, warm day would be the time when the temperature inversion begins to weaken as the sun heats up the cool air at and above the lake surface. The cool air over the lake thus begins to approach the stability point where normal convective mixing of surface air with air above can resume over the lake, just as it already has over the land since after sunrise ( Figure 4 C).

3. Any light breeze or puff of wind along the shoreline in these nearly calm conditions could set up a weak wind shear which will cause a slow counter swirl to form out in the air over the lake in any small bay along the shore. This swirl will be in both the warm air above the temperature inversion and in the cool surface air below it. The acceleration accompanying the curved flow of the weak swirl in the air initiates a small pressure and temperature drop.

V = n^1/2c_o [ 1 – T/T_o]^1/2 = n^1/2c_o [ 1 – (p/p_o)^2/7]^1/2

3. The angular momentum initiated by the wind shear along the shore is conserved as the air in the swirl flows spirally in towards the centre of the swirl in the bay. The flow speed towards the centre of the swirl must therefore also increase because of this conservation effect and the speed up further deepens the swirl’s pressure drop.

4. In most cases, with weak swirling motion the force of viscosity will act to weaken and perhaps dissipate any incipient vortex. But, in cases where the vortex occurrence also coincides with the cycle of restoration of normal convective motions over the lake in the late morning, then the cooling of the warm air flowing into the vortex will erase the inversion and the stability, and so can restore the lapse rate in the vortex core to the normal convective value. This would permit vertical convective flow to resume over the lake --- but only up through the vortex itself, where the expansive cooling has erased the warm inversion cap.

Thus the vortex, occurring at the right time of the surface air heating cycle over the lake can locally readjust the lapse rate in its funnel to the normal convective mixing value. The convective upwards flow then resumes- but only up through the vortex funnel (Figure 4 D).

This is somewhat analogous to the situation where water in a sink drains out through the drain hole under the force of gravity. In the case of the lake whirlwind, the air over the lake surface can locally ‘drain upward’, so to speak, through the vortex funnel under the force of convective buoyancy.

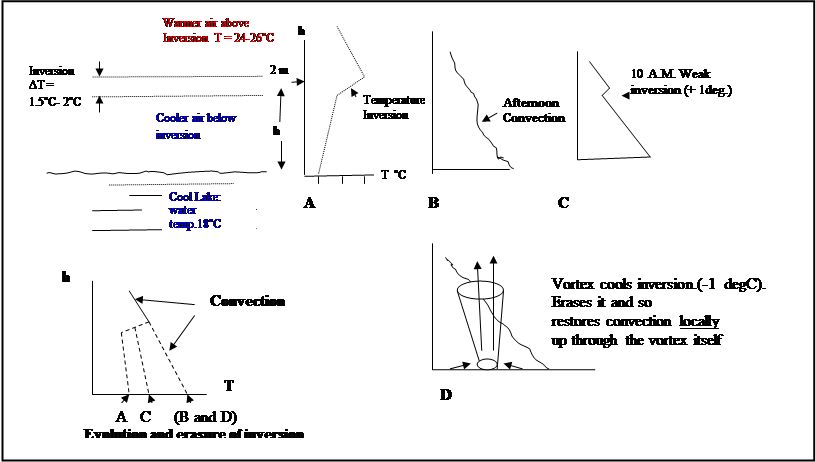
Fig. 4.Temperature inversion prevents convection (A and C), while ‘Erasure’ of inversion in vortex restores convection (D).

Conclusions: Part I

The study of the mini-whirlwind has led to the conclusion that the principal wind speed up process in the vortex is an adiabatic –isentropic linear expansion involving a small temperature, pressure and density drop accompanied by a very large wind flow increase.

The necessary initial swirl is set up by wind shear along the lake shore topography, and at a low level tempersture inversion over the lake, where the whirlwind formed.

The rarity of the phenomenon is due to the necessity to match all the elements of the whirlwind to the ‘window in time’ in the late morning when the restraining temperature inversion over the lake is not quite at the breakup stage in the daily heating cycle, that is to say at the point in time when the normal daytime vertical convective motions can resume. If the conditions do all match, then the swirl breaks the inversion cap in the vortex core and an upward convective flow can suddenly begin, channeled up through the vortex funnel to exit into the free air above the inversion.

The mechanism of isentropic flow speed up should apply to all whirlwinds, large and small. The inversion breakdown channeling a convective flow up through a vortex core may also apply to tornado funnel cloud formation on a cool dome’s inversion surface at a storm cloud’s base.

We now turn in Part 2 to the application of these insights to tornadoes.

Part 2. Tornado Dynamics, Intensity Limits and Intensity Prediction

Index

2.1 Vortex features in general

2.2 Vortex motions: The Rankine Combined Vortex

2.3 The source of the rotation needed in the vortex core

2.4 The driving pressure difference and ‘throughflow’ or mass flow rate of the tornado

2.5 Other types of tornado- like vortices

2.6 Satellite vortices, ‘sub- vortices’ or ‘suction’ vortices

2.7 Summary of the main tornado features.

2.8 A method of estimating tornado wind intensity limits from air mass humidity

2.9 A unifying vortex element: the flow condensation discontinuity

2.10 Conclusions

2.1 Vortex Features in General.

In general, atmospheric vortices appear to start as fluid rotation arising in a wind shear zone along a temperature discontinuity, in conflicting shearing flows inside a convective storm cloud, or from intersecting air outflows of different flow directions beneath a storm cloud [8,9]. Once the swirl of a vortex starts, the pressure in the swirl falls because of the acceleration and pressure force distribution in the curved air flow. The air flows spirally inwards toward the lower pressure at the vortex centre. At the same time, the conservation of angular momentum requires a speed up in the air flowing into the vortex at this ever diminishing radius. This angular momentum speed up follows from the relationship between vortex flow velocity V, rotation rate ω, and radial distance r from the vortex centre

V/r = ω = constant

whereby, as r decreases towards the centre of the vortex, the corresponding flow velocity V must increase to keep ω constant.

Once the swirl is started, it can be maintained or grow if there is a ‘throughflow’ of air driven by some overall pressure drop from flow source at the base of the vortex to its sink aloft, and if the rotation needed at the core can be supplied.

The following is a brief theoretical account of vortex structure and flow dynamics:

2. 2 Vortex Motions; The Rankine Combined Vortex

A Vortex involves organized circulatory or rotary motion of a fluid (i.e. liquid or gas) in which the fluid motion is round and round about a central point or central axis. The swirling motion of water slowly draining from a sink or wash basin is an example of a vortex. The flow around the perimeter of the basin and in the main body of the water in the wash basin is circulating, but it is not technically rotating. This seems a bit contradictory, but, for example, a floating cork which has a straight index line inscribed on its top, circulates around and round with the water, but the orientation of the line inscribed on the cork acts much as the needle of a compass and remains pointing in the same direction.. While the cork and the water it is floating in certainly do circulate, they do not themselves rotate. However, near the centre of the swirling water, if there is no actual gap in the fluid, the motion is different ---there the water core rotates in a wheel-like manner so that the rotation becomes zero at the central axis.

When the flow is steady, the outer, non-rotating circulation is described mathematically as

V_T r = Γ =constant

were Γ, with dimensions of angular momentum, is called the circulation, and V_T is the tangential velocity at any point of radius r. An example of this type of circulatory motion is the potential vortex, often called a free vortex, in which the motion can be described by a potential velocity function φ, such that dφ/dx = V [11 12]. The circulation of the water draining from a washbasin at points well away from the centre of the basin is an example of this potential vortex motion.

On the other hand, the true rotational motion in the inner core is called ‘solid’ or ‘wheel-like’ rotation, or sometimes, a forced vortex or rectilinear vortex, and is described mathematically as

V_T/r = ω

were ω is the rotation with the dimensions of frequency.

Atmospheric vortices typically consist of an outer circulatory whirl of irrotational or potential motion enclosing a very small inner core of solid rotation. The presence of the solid rotational core is physically necessary because a pure circulatory or potential vortex would require a velocity V of infinity at the core where r = 0, and so, in nature, some adjustment is necessary. This problem of infinity is avoided by a core having solid-like rotation, since then the velocity drops to zero at the central axis as required. The two flow systems 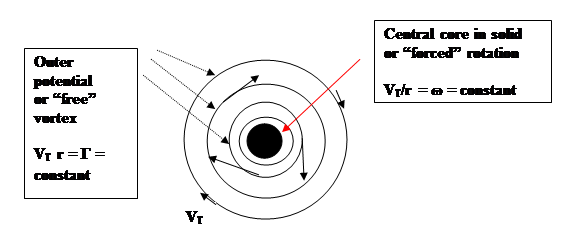taken together are often called a Rankine combined vortex [2,11,12 ].

ere n = 5Heremm

Figure 5. The Rankine Combined Vortex

2.3 The source of the initial rotation needed in the vortex core.

Vortex flow, with its angular momentum, swirl, or rotational motion cannot arise in a fluid spontaneously. As we have stated above, it must be formed at some shear surface or fluid discontinuity in one of several ways [1,2]. First, the boundary layer in any fluid flow has rotation because of the action of viscosity as the flow moves past the bounding surface, and also in the flow past a rounded edge. Across a discontinuity of any flow velocity, (Fig. 6) shear flow sets up small fluid vortices or fluid rotation which can then be entrained into the body of the fluid at a fluid boundary. As we shall discuss later, rotation can also arise from condensation of water vapour into cloud to form the tornado funnel. This last source has the advantage that the rotation emerges directly in the vortex core where it is essential to the vortex stability.

Figure 6. Formation of small vortices in a surface of discontinuity with shear flow

In the case of tornadoes, it appears that a principal source of the necessary initial fluid rotational motion is often the interaction between two different outflows of air beneath a storm cloud system as they meet and swirl at the earth’s surface. This applies in particular to interactions with the rear cool outflow or rear flank downdraft.

A principal source of such different cool outflows that can generate tornadoes in this manner is the local cooling of the air beneath convective shower clouds by shafts of falling rain, which partially evaporate and cool the air to form what is called a ‘cool dome’ of air beneath the rain cloud [8]. These cool domes typically have horizontal dimensions of a few kilometers. The surfaces of these cool domes are surfaces of the vorticity or rotation that can give rise to tornadoes.

In more detail, if the air beneath the shower cloud is at less then 100% humidity, as is usually the case, then some of the falling rain evaporates into the air and cools is by from 1 to say 5 deg C. The thin zone separating this dome of rain cooled air from the outside warm air, forms the temperature discontinuity or inversion surface we have mentioned. This temperature inversion surface (cool below, warmer aloft) is almost horizontal at the cloud base right beneath the cloud and slopes away to almost vertical at the leading edge of the cool dome at the ground, out ahead of the shower, as in a downdraft outflow. The shear across the discontinuity surface gives rise to a vortex sheet. As stated, two separate down flows of this rain cooled air, if and when they intersect, can generate the starting swirl needed for a tornado.

In some cases, tornadoes also seem to start on the surface of these sloping cool dome inversions under the cloud base, and then grow down from the cloud base along the curved dome to the ground.

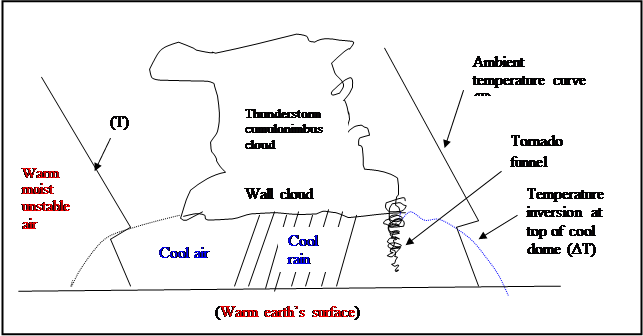
Fig. 7 Formation of a dome of cool air capped by a temperature inversion of 1 to 5 deg C beneath and out ahead of a thundershower cloud.

For completeness, we may note that another possible cause of rotation arises from instability waves on an atmospheric temperature inversion [12]. Such waves can become unstable and grow to form a vortex core.

2.4 The driving pressure difference and ‘throughflow’ or mass flow rate of the tornado

The tornado is driven by a pressure differnce Δp beween the ground level flow ( ‘source) and some flow exit level in the storm cloud interior alof (‘sink’).

The mass flow rate [ m-dot = dm/dt = ρVA = constant] up through the vortex is driven by the flow pressure gradient −Δp between the pressure in the core at the ground level and that in the convective storm cloud above where the funnel flow exits.

The pressure drop explanation and the tempersture drop explanations are equivalent, since in isentropic flow, as we have shown, the flow speed-up (+ΔV) is matched by a pressure, temperature and density drop ( − Δp, − ΔT, − Δρ ).

2.5 Oher types of tornado- like vortices

The principle other tornado- like vortices ones are waterspouts and dust devils [19 ]. The former are closely similar to tornadoes in mechanism but are considerably less-violent. Dust devils are highly convective, but have their origin at the heated ground level and are not associated with storm convective clouds,

In addition [20] there are the tornadoes, that form along the leading edge of cold air flowing out from under a thunderstorm or along a sudden wind shift line, which are sometimes called ‘gustnadoes’.

All these vortices, in order to be stable, are probably of the Rankine- Combined type discussed above. There is today a large amount of knowledge on this subject of atmospheric vortices and a close study of the literature is essential [e.g. 1,3,8, 9, 10].

2.6 Satellite vortices, ‘sub- vortices’ or ‘suction’ vortices

There are also cases of smaller vortices, or satellite tornado funnels, forming inside a tornado area and precessing rapidly around the main funnel as the tornado as a whole moves forward. These small satellite vortices are also called ‘subvortices’ or ‘suction vortices’. Where they do occur, they cause much more severe damage than the parent storm, their winds being the sum of the main tornado flow speed plus their own swirling speed around the main funnel. Winds of over 400 mph have been estimated from the quasi- circular trash and damage lines they leave behind within the main tornado path. [9a]. We shall not examine them in detail in our model, which applies to the more common, single funnel vortices [9].

These sub-vortices emerge from the base of a so-called ‘wall cloud’ structure which forms beneath some cumulonimbus storm clouds . This ‘wall cloud’ is a more or less vertical- sided cloud growth, and, once formed, it rotates, sometimes quite rapidly. It is from the base of one of these wall clouds that the multiple funnel cloud sub- vortices frequently appear, some of which may then grow downwards to reach the ground and become tornadoes.

It seems most probable that the ‘wall cloud’ consists of a cloud, forming in the expanding and cooling air of the potential circulating flow part of the Rankine-combined vortex, that is, in the circulational portion of the vortex surrounding the central rotational core. This would fit with the straight sided nature of the cloud, and its relationship to the funnel cloud of the central core of the vortex. Because of the cloud and its associated heat of condensation, the thermodynamic process of the inflow in the wall cloud portion of the tornado cannot be isentropic, but must, instead, involve the heat engine process.

2.7 Summary of the Main Tornado Model Features.

1. The atmospheric vortex, in general, may start as a large gentle circulating swirl having a central core in a state of fluid rotation, arising from the rotational flow already present in a shear zone, or along a temperature discontinuity, or in conflicting air flows beneath a convective storm cloud. Then, conservation of angular momentum brings about an initial speed up in the air flow into the vortex towards its core. This speed up follows from the relationship between vortex flow velocity, rotation rate ω, and radial distance from the vortex centre

V/ r = ω = constant

2. Once the vortex core forms, the inflowing moist, but initially cloud free air, expands linearly in the lower pressure towards the core centre. This flow expansion is isentropic, and so the accompanying increase in flow velocity is large [see Sect. 2 above and the isentropic relationships]. In this way, small amounts of internal heat energy of the atmosphere represented by temperature drops of only 1 to 5 degrees C, can, by means of the isentropic flow conversion, produce the observed tornado wind speeds of 90 to 250 mph (40 to110 m/s).

3. As the air continues to flow into the newly formed vortex, it expands isentropically and cools. When this cooling has lowered the temperature of the air flowing into the vortex to its dew point, i.e. when the relative humidity of the inflowing air reaches 100%, then cloud condensation occurs, and the vortex` becomes visible, first as the ‘wall cloud’ and then as the core ‘funnel cloud’ extending down from it. The thermodynamic process in the outer, cloud free potential motion section of the vortex is isentropic, while, in the wall cloud and the funnel cloud, it is the heat engine process.

We may note here that, while we have treated the vortex process as an isentropic flow energy conversion or equalization of small temperature differences between air parcels, we could also look at it from another point of view as being, first the setting up of a pressure gradient between two air parcels of slightly different air pressure , followed by the isentropic flow in response to the pressure gradient . The end result is the same, namely, the smoothing out of pressure differences by an isentropic expanding and cooling flow and greatly increased flow speed.

4. If we recall that the isentropic process is one of ‘no heat addition’, then, since the condensation of water vapour in the inflowing air to form the funnel cloud adds its latent heat of condensation (typically causing a rise in air temperature of 1 to 3 deg. C), the isentropic, tangential wind speed-up must cease once the funnel forms; and so the high speed- up phase of the tornado reaches its limit. Any further speed up is by the inefficient heat engine process, and this, as we have seen above in Part 1, produces only much smaller wind speed- up of a few tens of meters per second. (Two additional speed up mechanisms in the tornado base at the ground are discussed below).

Therefore, in this new model, the presence of a visible funnel cloud also signals that the tornado has ended its high speed-up phase.

5. Some additional speed- up at the ground, may, however, take place. At the ground, surface friction alters the flow to permit increased updraft in the so-called ‘corner flow’ in which the inflowing tangentially swirling air turns abruptly upwards to spiral helically around the core up towards the parent storm cloud above [9]. This abrupt turning requires an abrupt acceleration of the flow velocity and a further drop in pressure. However, the surface friction also slows down the ground level tangential flow, permitting some inward cross isobaric radial flow to set in. This frictional slowing of basic wind speed must be subtracted from the vector sum of the tangential plus corner wind speed.

In addition, multiple ‘suction vortices’, ‘satellite vortices’ or ‘sub-vortices’ may form with greatly increased wind speeds.

6. The above points may perhaps be further clarified if the basic physical processes are outlined from the equations of flow.

Euler’s equation for steady streamline flow can be written as

dp = −ρ d(V² /2 ) = −ρ VdV (4)

which, when integrated, becomes

∫ dp/ρ + V² /2 = constant along a streamline (4b)

(If we now treat the density as constant, i.e. if we treat the fluid as incompressible, which is nearly the case for low flow velocities, then the Bernouilli equation results

p/ρ + V²/2 = constant along a streamline

The use of the incompressible Bernouilli equation for a compressible fluid such as air, gives acceptable numerical results for slower flow calculations ( less than about Mach 0.3), but its concepts do not clearly show the fluid behaviour in adiabatic/isentropic flow, and so the full isentropic equations for determining the thermodynamic quantities p, ρ, T and V (Section 1.2 above) are recommended even for low flow velocities.

7. In the case of a very dry atmosphere, where no funnel cloud condensation would occur even with very low pressures and large temperature drop on expansion, the isentropic equations would apply right up to the sonic speed (330 m/s or just over 700 mph) and the complete compressible flow treatment of Abdullah [16] would apply.

Earlier researchers were unaware of any physical limit to the velocity of tornados, and so Abdullah [16] introduced the full compressible flow equations and proposed the sonic shock limit of around 313 m/s or 711 mph for tornado maximum speed. With later observations that the top speed seemed to be about 135 m/s, the problem of the physical reason for this speed limit arose again, and is explained here via the condensation process which forms the tornado funnel cloud and at the same time puts an effective limit to the funnel wind speed.

8. As to the hollow core structure of many tornado funnels, this is explained by Kangieser [17] as a centrifugal effect of the high speed rotation in the funnel. The cloud droplets are forced outward from the tornado core by centrifugal force to reach an equilibrium radial distance, leaving the core empty of cloud droplets..

9. The main elements of a tornado are depicted in Figure 8:

(1) a cloud free rotational core in which V/r = ω = constant.

(2) a condensate sheath surrounding the core which constitutes the visible tornado funnel cloud .This funnel or cloud sheath is highly turbulent with small eddies about a meter or so in diameter, and which themselves are rotating and swirling helically around the hollow core [18]. Flow transformations in this sheath are non-isentropic and the heat engine process with only small velocity speed up prevails.

(3) Outside the funnel cloud or condensate sheath is a much larger diameter, cloud –free, swirl area which is the Potential Vortex or ‘free vortex’ region. The flow in it is in a state of circulation but is not rotational. Flow transformations are isentropic in this cloud- free region, and so this is the region of fastest wind speed up, reaching a maximum tangential velocity right at the visible funnel outer surface. From there inwards to the core the tangential velocity decreases.

The whole tornado, outer plus inner core comprises a Rankine- Combined Vortex.

Figure 8. Rankine- Combined Vortex Model of the Tornado

2.8 A Method of Estimating Tornado Wind Intensity Limits from Air Humidity

Our analysis so far has shown that there are two distinct flow speed-up mechanisms in tornados which produce very different wind speeds from conversion of any given heat or temperature differential ΔT. We can combine these two different flow processes to model the life cycle and intensity levels of a tornado.

First, as we have shown above, when the shear flow at a temperature discontinuity in the cloud free atmosphere develops into a vortex, the inflowing air accelerates isentropically, so that the resulting tangential velocity developed in the outer cloud free portion of the vortex is large even for small temperature drops; for example a 1 deg in flow temperature results in a 42.9 m/s tangential swirling wind speed ( i.e. 98 mph), 2 deg. C gives 60.7 m/s or 136 mph. The eventual tangential velocity or intensity that is reached is limited only by the amount of the temperature drop and pressure drop in the inflowing cloud-free air. The vortex at this stag is invisible with no funnel yet formed.

Table 2

Isentropic Tangential Wind Speed Resulting From Various Atmospheric Temperature Transformations

T_o T₁ ΔT(_spread) Tangential Velocity V_T = n^1/2 c_o [ΔT_spread /T_o]^1/2

____________________________________________________________

303 ˚K 302˚K 1˚C 42.9m/s 96.0 mph

303 301 2 60.7 135.7

303 300 3 74.3 166.2

303 299 4 85.8 192

303 298 5 95.8 214.6

303 297 6 105.1 235.1

303 296 7 113.5 253.9

303 295 8 121.3 271.5

303 294 9 128.7 287.9

303 203 10 135.7 303.5.

Notes

1. n = 5

2. c_o = 334 m/s = sound speed at m.s.l.

Second, when the inflowing, accelerating, expanding air in the vortex cools to the dew point T_{d ,} that is to say, when the relative humidity R.H. reaches 100% and condensation of liquid cloud water takes place, the tornado funnel cloud appears. This condensation releases latent heat of condensation into the flowing air, and so the isentropic speed up mechanism ceases in the cloudy funnel, and is replaced in the funnel by the inefficient heat engine speed process.

Thus, the tornado intensity or speed up growth rate slows down markedly when the visible funnel cloud forms and the tornado intensity slows or stabilizes. .

The end result, is that a vortex velocity limit emerges, consisting of the sum of the isentropic initial large flow speed increase plus the much smaller heat engine speed increase after the funnel cloud formation. For example, an isentropic conversion of a 1 degree C of cloud free dry air inflow would give a flow velocity of 43.9 m/s (96.0 mph) mph. The latent heat of condensation released by the funnel cloud forming is, for example about 2 deg C: this added heat, if converted to flow velocity by the heat engine process, would add only another 1.59 m/s or 3.6 mph, for a sum total limiting speed of 45.9 m/s or 102 mph. Other combinations of clear and cloudy air speed up can be found in Table 3.

Table 3.

Examples of Tornado Limit Velocity with Various Humidities (T_o – T_D)

T_o T_core ΔT T_D T_o– T _D T_D -T_c Isentropic Vel. Heat Engine Vel. Limiting Vel. (sum)

303 K 302 1 302.5 0.5C 0.5 30.3 m/s 1.29 m/s 31.6 m/s 71mph

303 301 2 302 1 1 42.9 2.58 45.5 102

303 300 3 301 2 1 60.7 2.58 63.3 142

303 299 4 300 3 1 74.3 2.59 77 172

303 298 5 299 4 1 85.8 2.59 88 198

303 293 10 294 9 1 128.7 2.61 131 294

T_o – Ambient warm air mass temperature

T_core – Cool core temperature

ΔT - Total temperature differential available for conversion into vortex tangential flow velocity

T_D – Dew point of inflowing air mass ( A measure of relative humidity, R.H.)

T_{o –} T_D – Amount of cooling possible in in-flowing clear air, until funnel cloud forms or is entered by the inflow, and which is available for isentropic conversion into high tangential increases in flow speed

T_D – T_core - Amount of cooling possible inside funnel cloud and which is available for heat engine conversion into much lower tangential increases in flow speed.

Isentropic Vel. Flow velocity reached by isentropic conversion of temperature difference in clear unsaturated air (see Table above)

Heat Engine Vel. – Additional Flow velocity added by heat engine conversion of remaining temp difference between saturated air inside funnel cloud and cool core temperature (see Table 1)

Speed conversion factor: m/s x 2.2369 = mph

Since the heat engine component of the speed up in the cloudy air in the funnel is small compared to the isentropic component of speed up , a simple close approximation to the limiting, or top tangential wind speed of a tornado, can be calculated from the isentropic speed equation alone:

V_T = n^1/2 c_o [1 – T_D/ T_o ]^1/2

V_T = 2.236 x 334 x [1 – T_D/ T_o ]^1/2 (mph) (1)

where T_D is the dew point and T_o is the temperature of the ambient air mass surrounding the tornado and feeding into it.

Thus, on any likely tornado day, from a forecast of the expected air temperature T_o and dew point temperature T_D, the use of this equation will give an estimate of the probable maximum tornado wind speed or tornado intensity for that particular locality.

[This simple tornado intensity predictor should be readily testable for validity against historical tornado occurrence records and concurrent air mass temperatures and humidity.]

Additional tornado funnel speed-up at ground level.

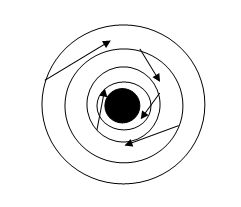
When the tornado funnel cloud ‘touches down’ and reaches the earth’s surface, then the surface friction slows the flow and it turns a bit inward towards the core and across the circular isobaric or pressure pattern, Fig. 9 .

This inflow leads to the so-called ‘corner flow’ [9] speed-up, where the radial, cross isobaric flow into a tornado at the ground must turn abruptly upward towards the vertical at the core boundary in order to spiral up towards the storm cloud , and so must accelerates greatly.

Fig. 9. Surface friction turns the flow

Radially inward across the isobars towards the core centre.

The corner flow and the so called ‘suction vortices’ if present will locally add to any general velocity predictions made from the dew point spread of Table 2. The slow down from surface friction at ground level will of course subtract from the speed up effects.

2.9 A Unifying Vortex Element: The Flow Condensation Discontinuity

We can now reconcile how a non- rotational, outer tornado region fits smoothly into, and interacts with, an inner rotational core ,.

Once condensation and the accompanying release of latent heat into the air takes place, the air flow where the air from the outer ‘potential vortex’ enters the ‘forced vortex’ of the funnel is no longer smooth and laminar, but becomes disordered and turbulent and its entropy increases significantly. It also has become rotational, so that it is now in the same rotational state as that which prevails in the vortex core of the Rankine combined vortex. In this way, the now cloudy, rotational air flow becomes smoothly incorporated into the already rotational inner core flow.

In this way, we can integrate smoothly the circulating non-rotational air flowing from the outer portion of the tornado, into the vortex core which has opposite rotational fluid properties, so as to now explain how the combined vortex in nature is a unified, stable, dynamic flow system.

To repeat, fluid angular rotation (ω) is necessary for stable motion in the core of an atmospheric vortex, such as the Rankine-combined model described. Since this necessary angular motion cannot arise spontaneously in a fluid, its source in tornadoes, waterspouts, dust devils and the like, is a matter of importance for understanding their motions, and hopefully, even for predicting their occurrence and intensity. As we have stated above, some undoubted initial startup fluid angular momentum arises from shearing flow at the interface between different local air mass outflow velocities beneath storm cloud systems, from shear along a temperature inversion surface, from friction induced shear flow in the atmospheric boundary layer at the earth’s surface, and so on.

There is one additional rotational case that invites further attention as to its role in tornadoes. This is the flow rotation that is needed during the tornado funnel cloud formation and its growth from the parent wall cloud towards the ground. This growth towards the ground may be steady and take a few minutes to be completed. Even more often, however, the funnel wavers in its downward growth, before slowly retreating upwards to be adsorbed into the parent wall cloud from which it emerged. The impression of some imbalanced interplay of opposing physical processes is strong. A process that involves both funnel cloud formation and the in situ emergence of the necessary rotation is the water vapor condensation process that forms the funnel cloud. This condensation occurs in the inflowing air as it enters the vortex core. Here, the amount of cooling of the air in the vortex core at the funnel cloud’s tip, is determined by the extent of adiabatic expansion and consequent cooling in the core.

Now, if the moisture content of the inflowing air, as evidenced by its dew point temperature, is higher than the vortex core temperature at the growing vortex tip, then the inflowing air will be cooled below its dew point at the funnel’s tip, further cloud condensation will take place, and the tornado funnel cloud will continue to grow and extend downward toward the ground,

On the other hand, if the dew point temperature of the air flowing into the funnel tip core is lower than the core temperature, then no new condensation will occur and the funnel cloud growth will stop. Depending on the relative humidity of the inflowing air, the funnel cloud may even start to evaporate and slowly retreat upwards to be re- adsorbed by the parent storm cloud from which it earlier emerged when more moist conditions existed in the air beneath the storm cloud.

In this way, the humidity of the air beneath the wall cloud would appear to control the formation and growth of the tornado funnel towards its touchdown at the ground, as well as controlling its general intensity limits, and automatically furnishing the necessary solid rotation right in the core itself.

-

3.0 Conclusions

1. A fortuitous encounter with a very rare type of mini-tornado which occurs under very simple, fine weather conditions has yielded insights into its origin, structure and growth which appear to be applicable to the full scale tornadoes of convective storms.

2. All tornadoes require (1) a source for initiating a ‘solid’ rotational or vortical swirl motion, which becomes the tornado core, and (2) an outer circulation of air flow around the rotational core which is isentropically transformed into a high speed tornadic flow as it expands and cools while flowing in towards the funnel and (3) a continuous throughflow of air from a source, usually at the ground, to a sink in the convective storm cloud aloft. This vertical mass throughflow is sustained by the pressure differential −Δp between ground level pressure and the pressure aloft at the discharge level into the storm cloud.

3. In the case of the mini-tornado, the source of the initial rotation or swirl is likely a weak wind flow past the shoreline irregularities, and/or an instability wave on the temperature inversion surface that forms over the cool lake in nearly calm, warm weather during the heat of the day.

In the case of full scale, storm cloud tornados, the originating swirl can be due to wind shear from flow past surface topography beneath the storm cloud, or from shear interaction within or between two cool outflows from beneath large thunderstorms, especially beneath super- cell thunderstorms [8], or from internal swirling flows within the wall cloud.

4. We now have explanations for (a) the turbulent rotational sheath at the edge of the funnel cloud, (b) for the smooth merger of the two types of vortex flow, namely the outer circulating flow with the inner rotating flow, and (c) for the observed general speed limitation of the tornado to around 300 mph or 135m/s

5. On any likely tornado day, from a forecast of the expected air temperature T_o and dew point temperature T_D, the relative humidity appears to provide an estimate of the probable maximum tornado wind speed, or general tornado intensity, for that particular locality and day.

This simple tornado intensity predictor should be readily testable for validity against records of historical tornado occurrence and concurrent air mass temperatures and humidity.

6. We also have a source for the inner core rotation of the tornado emerging in the flow at the condensation discontinuity at the funnel cloud, where the inflowing air from the outer potential vortex not only condenses some of its moisture to form the funnel cloud but also releases rotational flow into the core, to thereby stabilize the vortex motion.

References

1. The Tornado: Its Structure, Dynamics, Prediction and Hazards. Church, C., Burgess, D., Doswell, C. A., Davies-Jones, R., (eds.). AGU Monograph 79, American Geophysical Union. Washington, D.C., 1993.

2. Munson, Bruce R., Young, Donald F., and Okiishi, Theodore, H., Fundamentals of Fluid Mechanics, John Wiley & Sons, New York, 1990.

3. Doswell, Charles, A.111, and Burgess, Donald, W. “Tornados and Tornadic Storms: A Review of Conceptual Models”. In AGU Monograph 79, American Geophysical Union. Washington, D.C., 1993.

4,5. Rossman, Fritz O., “Waterspouts and Tornados”, Weather, pp. 104-106, March 1956. Royal Meteorol. Soc., London [and in Monthly Weather Review, 48, p.351, May 16, 1920, “Observations on Lake Newcombe, Adirondack Mountains , N.Y”.].

6. : Tornado-genesis by an Isentropic Transformation of Heat Differences into Wind Speed

7. Vonnegut, Bernard, “Electrical Theory of Tornados”. J. of Geophysical Res. 65, 1, pp 203-212, Jan. 1966.

8. Purdom, James, F.W. “Satellite Observations of Tornadic Thunderstorms”, In The Tornado: Its Structure, Dynamics, Prediction and Hazards. Church, C., Burgess, D., Doswell, C., Davies-Jones, R., (eds.). AGU Monograph 79, American Geophysical Union. Washington, D.C., 1993.

9. Lewellen, W.S., “Tornado Vortex Theory”. In: AGU Monograph 79, American Geophysical Union. Washington, D.C,. 1993.

10.. Fujita, T.T., and B.E. Smith, “Aerial Survey and Photography of Tornado and Microburst Damage” in AGU Monograph 79, American Geophysical Union. Washington, D.C. 1993.

11. Shapiro, A.H., The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 Vols., Wiley and Sons, New York, N.Y., 1953.

12. Prandtl, L. and O. G. Tietjens, Applied Hydro- and Aeromechanics, Dover Publications Inc., New York, 1957.

13. Lamb, Sir Horace. Hydrodynamics. Dover Publications Inc. New York, 1931.

14. Brunt , David, Physical and Dynamical Meteorology. Cambridge University Press, 1941.

15. Rankine, W. J., A Manual of Applied Mechanics, , Charles Griffin, London, 1882.

16. Abdullah, A.J., “Some Aspects of the Dynamics of Tornadoes”. Monthly Weather Review, 83, 4, pp. 83-94, April 1955.

17. Kangieser, Paul C., “A Physical Explanation of the Hollow Structure of Waterspout Tubes”. Monthly WeatherReview, 82, 6, pp. 147-152, June 1954.

18. Golden, J, H., “The Life-cycle of Florida Keys’ Waterspouts”, J. Appl. Meteorol., 13 667-692 and 693-709, 1974.

19. Idso, Sherwood, B., “Tornado or Dust Devil: The Enigma of Desert Whirlwinds”. American Scientist, 62, 530-541, Sept. – Oct. 1974.

20. Bluestein, Howard A. and Joseph H. Golden, “A Review of Tornado Observations”. AGU Monograph 79, ( Ref. 3 above) pp. 319 -352. 1993.

22. By isentropic we mean ‘a thermodynamic process occurring without any heat energy input into or output from the system’; the energy for the change comes from the internal energy of the system. For example, in an isentropic flow acceleration of a gas, the internal energy supplies the work needed and this shows up as a drop in the gas temperature, pressure and density accompanying the flow velocity increase. Such an expansion is also called an adiabatic expansion. If the process is reversible, with the thermodynamic variables of pressure, temperature and density returning to their original values upon compression, then the process is not only adiabatic but reversible and so is isentropic. In the present work, we are concerned with dynamic flow expansions of gas rather than the static or volume expansions at zero flow. And so, even though the processes are probably not reversible, I have preferred to use the term isentropic process to describe the adiabatic flow changes since the appropriate unambiguous and convenient equations are the isentropic ones. The use of the term adiabatic might lead to some confusion that the process is a static volume expansion rather than a linear expansion accompanying a flow velocity increase.

Acknowledgement

I gratefully acknowledge the many years of essential encouragement from my dear wife, recently sadly deceased. She was the one to spot the mini-vortex which had so quietly and suddenly appeared. She was also the one who drew my attention away from fishing just in time for me to take in its astonishing essentials before it suddenly vanished. In spite of the difficulties and demands of advancing age, she never wavered in her conviction that I should pursue an explanation for this strange event.

Copyright © 2013 Bernard A. Power

Back to Main Page